Lab 03: Power & Sample Size Planning
Aug 24, 2022
เกริ่นนำ
ในการทดสอบสมมติฐานว่าง (null hypothesis significant testing) อิทธิพลที่ผู้วิจัยกำลังศึกษาอาจมีอยู่จริง (\(H_0\) เป็นเท็จ) แต่ผลการวิเคราะห์ทางสถิติกลับไม่ถึงระดับนัยสำคัญ จึงไม่สามารถปฏิเสธสมมติฐานว่างได้ (fail to reject $H_0$) กรณีที่การวิเคราะห์ทางสถิติมีกำลังไม่พอที่จะปฏิเสธสมมติฐานว่างนี้ เรียกว่า Type II error เราใช้ \(\beta\) เป็นสัญลักษณ์แทนความน่าจะเป็นที่ว่า หากสมมติฐานว่างไม่เป็นจริง มีความน่าจะเป็นเท่าใดที่เราจะสังเกตได้ค่าสถิติที่ไม่ถึงระดับนัยสำคัญทางสถิติ การเกิด Type II error ทำให้ผู้วิจัยสรุปว่าไม่พบความแตกต่างทั้งที่ความแตกต่างมีอยู่จริง หรือ ที่เรียกว่า ผลลบลวง (false negative)
การลด Type II error (\(\beta\)) ก็คือการเพิ่มกำลังทางสถิติ (power; \(1-\beta\)) ในขณะที่ค่า Type I error (\(\alpha\)) มีธรรมเนียมกำหนดไว้ที่ .05 ค่ากำลังทางสถิติมักถูกกำหนดอยู่ระหว่าง .80 - .90 ขึ้นอยู่กับผู้วิจัย
เพื่อให้ได้กำลังทางสถิติที่เพียงพอต่อการทดสอบสมมติฐาน นักวิจัยสามารถดำเนินการได้หลายอย่าง เช่น พยายามควบคุมปัจจัยแทรกซ้อนเพื่อให้ได้ผลที่คงที่มากขึ้น พยายามให้กระบวนการจัดกระทำที่ทำให้เกิดผลชัดเจนหรือเกิดความแตกต่างมาก ๆ หรือพยายามเพิ่มกลุ่มตัวอย่างให้มากขึ้นเพื่อลดความคลาดเคลื่อนจากการสุ่มตัวอย่าง เป็นต้น
การวิเคราะห์กำลังทางสถิติ(power analysis) ขึ้นอยู่กับพารามิเตอร์ 4 ตัวได้แก่
- ขนาดกลุ่มตัวอย่าง
- ขนาดอิทธิพล
- ระดับค่า \(\alpha\)
- ระดับค่ากำลัง
โดยปกติผู้วิจัยจะกำหนดค่า alpha และค่า power ที่ต้องการไว้ เช่น \(\alpha = .05\) และ power = .80 เป็นต้น ดังนั้นผู้วิจัยจึงเหลือต้องควบคุมพารามิเตอร์อีกสองตัวที่เหลือเพื่อให้ได้ค่า power ที่ต้องการ
ในการออกแบบการทดลอง ผู้วิจัยมักจะอ้างอิงรูปแบบการทดลองจากงานวิจัยที่ผ่านมา ด้วยเหตุนี้ผู้วิจัยจึงพอจะทราบได้ว่าผลการทดลองที่ผ่าน ๆ มีขนาดอิทธิพลประมาณเท่าใด (บางครั้งก็อ้างอิงได้จากการวิเคราะห์อภิมาน meta-analysis) ดังนั้นจึงเหลือพารามิเตอร์ตัวสุดท้าย นั่นคือ เราต้องใช้กลุ่มตัวอย่างขนาดเท่าใดจึงจะได้ขนาดกำลังที่ต้องการ
ด้วยเหตุนี้ การวางแผนออกแบบการวิจัยเพื่อทดสอบสมมติฐาน ผู้วิจัยจึงควรต้องศึกษาขนาดอิทธิพลของงานวิจัยในอดีตเพื่อใช้วิเคราะห์กำลังทางสถิติ แล้วกำหนดว่างานวิจัยของตนนั้นจำเป็นต้องใช้กลุ่มตัวอย่างขนาดเท่าใด (งานวิจัยที่มีกำลังไม่พอ มีความเป็นไปได้สูงที่จะทำแล้วเสียเปล่า เพราะแม้ว่าจะมีอิทธิพลอยู่จริง ก็มีโอกาสสูงที่จะไม่พบความแตกต่างที่มีนัยสำคัญ)
ในแบบฝึกหัดนี้เราจะได้เรียนรู้การวิเคราะห์กำลังทางสถิติเพื่อกำหนดจำนวนกลุ่มตัวอย่างโดยใช้
G*Power และ pwr package ใน R
1. G*Power
G*Power เป็นโปรแกรมที่พัฒนาโดยกลุ่มนักวิจัยจาก Heinrich-Heine-Universität Düsseldorf โปรแกรมนี้มี GUI (graphic user interface) ที่ใช้งานง่ายเน้นการคลิก ไม่ต้องเขียนโค้ด และครอบคลุมการวิเคราะห์กำลังสำหรับสถิติที่เป็นที่นิยมค่อนข้างครบถ้วน ดาวน์โหลดโปรแกรมที่นี่
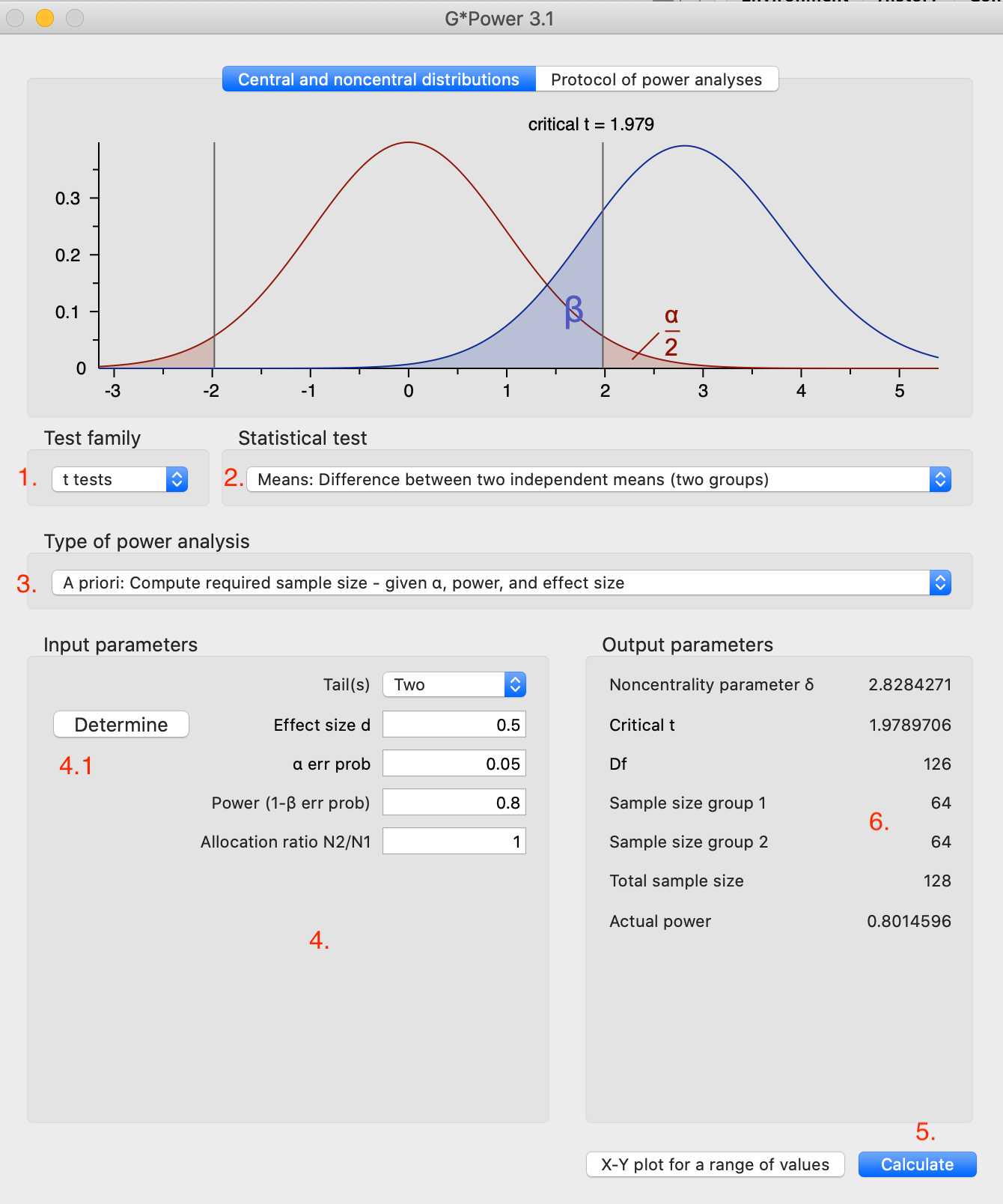
G*Power
องค์ประกอบในหน้าต่าง
- เมนู Test family ใช้สำหรับเลือกกลุ่มของสถิติทดสอบ เช่น t tests, F tests, \(\chi^2\) test เป็นต้น
- เมนูสถิติทดสอบ Statistical test ใช้เลือกสถิติที่เฉพาะเจาะจงกับการวิเคราะห์ที่ผู้วิจัยต้องการ เช่น independent t-test, one sample t-test, paired t-test, หรือ การทดสอบสัมประสิทธิ์ถดถอยแต่ละตัว เป็นต้น
- เมนูเลือกชนิดการวิเคราะห์กำลัง (Type of power analysis) โดยปกติแล้วเราจะเลือก “A priori: Compute required sample size” เพื่อคำนวณจำนวนกลุ่มตัวอย่าง
- Input parameters
- Tail(s): เลือกว่าการทดสอบเป็นแบบหางเดียว หรือสองหาง
- Effect size: ค่านี้จะแตกต่างกันไปตามสถิติที่ต้องการ ในตัวอย่างด้านบนเป็นการทดสอบความแตกต่างของค่าเฉลี่ยด้วย t-test ขนาดอิทธิพลที่โปรแกรมนี้ใช้คือ ค่า Cohen’d (หากนำเมาส์ไปวางบนกล่อง จะปรากฏขนาดอิทธิพลตามธรรมเนียมปฏิบัติไว้ใช้อ้างอิง) 4.1 ปุ่ม Determine หากเราไม่ทราบค่า effect size โปรแกรมสามารถช่วยคำนวณให้จากข้อมูลอื่น ๆ เช่น M, SD, n ของแต่ละกลุ่ม ซึ่งมักหาได้ไม่ยากจากบทความ (เช่น ตาราง descriptive statistics)
- \(\alpha\) err prob: กำหนดค่า alpha โดยปกติจะเป็น .05
- Power: กำหนดค่า power ที่ต้องการใช้ในการวิจัยของเรา โดยมากมักจะอยู่ระหว่าง .80 - .90
- Allocation ration N2/N1: เมนูหลังจากนี้จะเปลี่ยนไปตามสถิติที่ใช้ ในตัวอย่างนี้ คือ การระบุสัดส่วนของกลุ่มตัวอย่างในสองเงื่อนไข หากสองเงื่อนไขมีกลุ่มตัวอย่างเท่ากัน ให้ค่านี้เป็น 1
- ปุ่ม Calculate
- จำนวนกลุ่มตัวอย่างที่ต้องใช้และพารามิเตอร์อื่น ๆ จะปรากฏที่กล่องนี้
1.1 Independent t-test with known effect size
สมมติว่าผู้วิจัยต้องการศึกษาปรากฏการณ์ ego-depletion โดยใช้งานขีดฆ่าตัวอักษร (crossing out letters task) ซึ่งมีการวิเคราะห์อภิมานว่ามีขนาดอิทธิพลเท่ากับ .77 (Hagger et al., 2010) ผู้วิจัยจำเป็นต้องใช้กลุ่มตัวอย่างเท่าใดเพื่อที่จะพบผลที่มีนัยสำคัญทางสถิติ หากปรากฏการณ์นี้มีอยู่จริง
- เลือก t-test ในช่อง Test family
- สมมติให้ออกแบบการทดลองแบบระหว่าง 2 กลุ่ม (ทดลอง-ควบคุม) ให้เลือก “Means: Difference between two independent means (two groups)” ซึ่งเป็นคำอธิบายของการทดสอบ independent t-test
- เลือก Type of power analysis เป็น “A priori: Compute required sample size - given \(\alpha\), power, and effect size”
- ใน input parameters
Tail(s): เลือกเป็น One เนื่องจากเรามีทิศทางที่ตั้งสมมติฐานชัดเจน (หากไม่แน่ใจให้เลือก Two)
Effect size d = .77 ตามค่าที่ค้นคว้าได้จากงานวิจัย
\(\alpha\) err prob = .05 ตามธรรมเนียม
Power (1 - \(\beta\) err prob) = .90
Allocation ration N2/N1 = 1 ออกแบบเป็น balanced design กลุ่มตัวอย่างในสองเงื่อนไขเท่ากัน
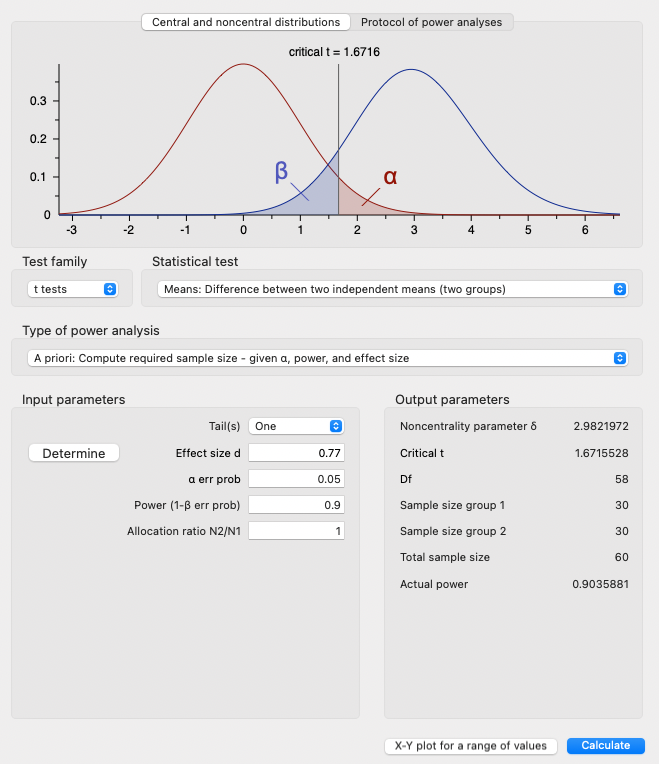
G*Power with known effect size d
เพื่อให้ได้ power = .90 โดยเชื่อว่า effect size d = .77 จะต้องใช้กลุ่มตัวอย่างเงื่อนไขละ 30 คน ค่าวิกฤติของสถิติทดสอบ t คือ 1.672
1.2 Independent t-test with known M and SD
หากงานวิจัยที่เราใช้อ้างอิงไม่ได้รายงานค่า effect size d เราสามารถคำนวณขนาดอิทธิพลได้จากค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของแต่ละกลุ่ม สมมติว่าในการทดสอบจำนวนคำที่ผู้เข้าร่วมการทดลองจำได้ เปรียบเทียบระหว่างเงื่อนไขทดลอง (M = 13.46 คำ, SD = 4.35) และเงื่อนไขควบคุม (M = 11.23 คำ, SD = 3.85) ให้
- กดปุ่ม Determine ข้างหน้าช่อง Effect size d
- กรอกค่า M และ SD
- กดปุ่ม Calculate เพื่อดูขนาด effect size หรือ กด Calculate and transfer to main window เพื่อนำข้อมูลไปกรอกในช่อง Effect size d
- กด Calculate ในหน้าต่างหลักเพื่อคำนวณ Sample size
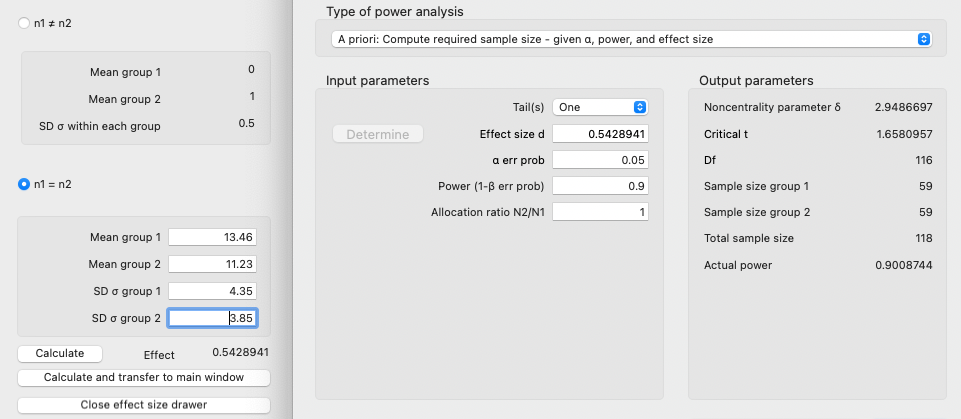
G*Power with M and SD
2. pwr package
#install.packages("pwr")
library(pwr)อ่านคำแนะนำ package ได้ที่นี่.
pwr package มีคำสั่งวิเคราะห์กำลังสำหรับสถิติทดสอบหลัก ๆ ได้แก่
pwr.p.test: one-sample proportion testpwr.2p.test: two-sample proportion testpwr.2p2n.test: two-sample proportion test (unequal sample sizes)pwr.t.test: two-sample, one-sample and paired t-testspwr.t2n.test: two-sample t-tests (unequal sample sizes)pwr.anova.test: one-way balanced ANOVApwr.r.test: correlation testpwr.chisq.test: chi-squared test (goodness of fit and association)pwr.f2.test: test for the general linear model
สำหรับการออกแบบที่ซับซ้อน เช่น factorial design หรือ repeated-measure design เราจะต้องใช้ package อื่น
2.1 Known effect size
เราจะใช้คำสั่ง pwr.t.test สำหรับตัวอย่าง independent
t-test เรื่อง ego-depletion ด้านบน
คำสั่งนี้เรามี argument ตามด้านล่าง
pwr.t.test(n = NULL,
d = NULL,
sig.level = 0.05,
power = NULL,
type = c("two.sample", "one.sample", "paired"),
alternative = c("two.sided", "less", "greater"))เนื่องจากเราต้องการกำหนดจำนวนกลุ่มตัวอย่าง n เราจะไม่ใส่ argument
นี้ในคำสั่ง
กำหนดเฉพาะ d, power, type, และ
alternative ตามตัวอย่างด้านล่าง
pwr.t.test(d=.77, sig.level=.05, power = .9, type = "two.sample", alternative = "greater")##
## Two-sample t test power calculation
##
## n = 29.58978
## d = 0.77
## sig.level = 0.05
## power = 0.9
## alternative = greater
##
## NOTE: n is number in *each* groupเราจะได้ค่า n ออกมา (สำหรับแต่ละเงื่อนไข) จากนั้นปัดเศษ จะได้เท่ากับที่คำนวณด้วย G*Power
2.2 Known M and SD
เริ่มต้นด้วยการคำนวณ effect size Cohen’s d ด้วยสูตรด้านล่าง (กรณีกลุ่มตัวอย่างเท่ากัน)
\[ d = \frac{\bar{X}_1 - \bar{X}_2}{s_{p}} = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s_1^2+s_2^2}{2}}} \]
d <- (13.46 - 11.23)/sqrt((4.35^2 + 3.85^2)/2)
d## [1] 0.5428941pwr.t.test(d=d, sig.level=.05, power = .9, type = "two.sample", alternative = "greater")##
## Two-sample t test power calculation
##
## n = 58.80131
## d = 0.5428941
## sig.level = 0.05
## power = 0.9
## alternative = greater
##
## NOTE: n is number in *each* group2.3 Plotting a power graph
เราสามาถใช้คำสั่ง plot()
เพื่อแสดงภาพความสัมพันธ์ระหว่างจำนวนกลุ่มตัวอย่างกับขนาดกำลัง
ภายใต้เงื่อนไขพารามิเตอร์ที่กำหนด
medium_power <- pwr.t.test(d=.5, sig.level=.05, power = .8, type = "two.sample", alternative = "two.sided")
plot(medium_power)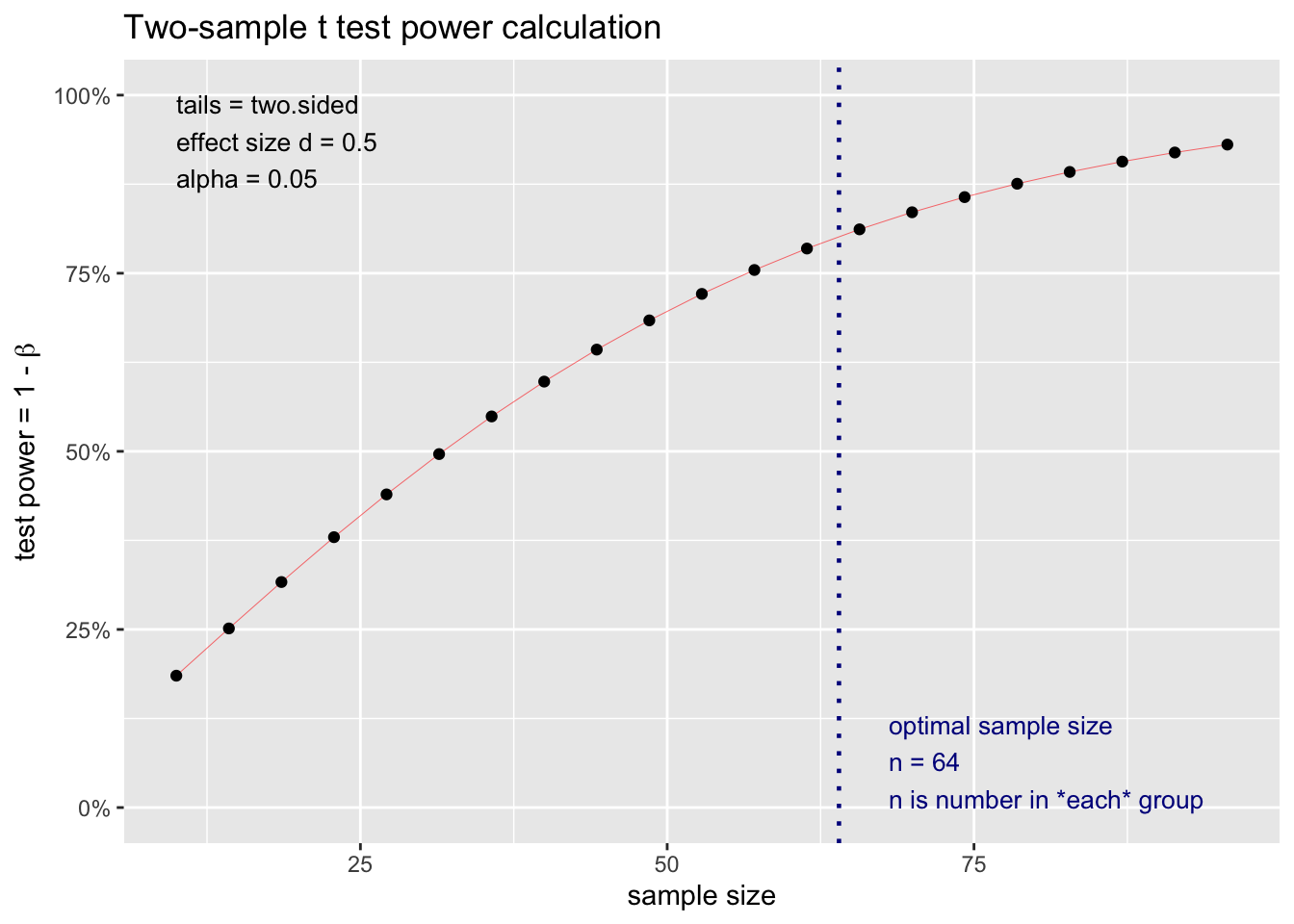
4. Other power functions
One-way ANOVA
คำสั่ง pwr.anova.test ใช้คำนวณกลุ่มตัวอย่างสำหรับ one-way ANOVA
ได้ โดยเราจะต้องกำหนดจำนวนกลุ่มในการเปรียบเทียบ k, effect size
แบบ Cohen’s f , และระดับ power ที่ต้องการ
library(pwr)
pwr.anova.test(k = 3, f = .25, power = .8) # An example of medium effect size with three conditions. ##
## Balanced one-way analysis of variance power calculation
##
## k = 3
## n = 52.3966
## f = 0.25
## sig.level = 0.05
## power = 0.8
##
## NOTE: n is number in each groupCopyright © 2022 Kris Ariyabuddhiphongs