Lab 10: Hierarchical Regression
Kris Ariyabuddhiphongs
Mar 30, 2022
# load all packages for this tutorial
library(psych)
library(car)
library(carData)
#install.packages("fastDummies")
library(fastDummies)1. Explore Data
pmi = presumed media influence รู้สึกว่าสื่อมีอิทธิพลแค่ไหน
import = ความสำคัญของประเด็น (น้ำตาลขาดตลาด)
reaction =
ผู้เข้าร่วมการวิจัยเห็นว่าตนเองมีโอกาสจะตอบสนองมากน้อยแค่ไหน (เช่น
จะไปซื้อน้ำตาลมาเก็บไว้)
data(Tal.Or)
media <- Tal.Or
head(media)## cond pmi import reaction gender age
## 1 1 7.0 6 5.25 1 51
## 2 0 6.0 1 1.25 1 40
## 3 1 5.5 6 5.00 1 26
## 4 0 6.5 6 2.75 2 21
## 5 0 6.0 5 2.50 1 27
## 6 0 5.5 1 1.25 1 25boxplot(media)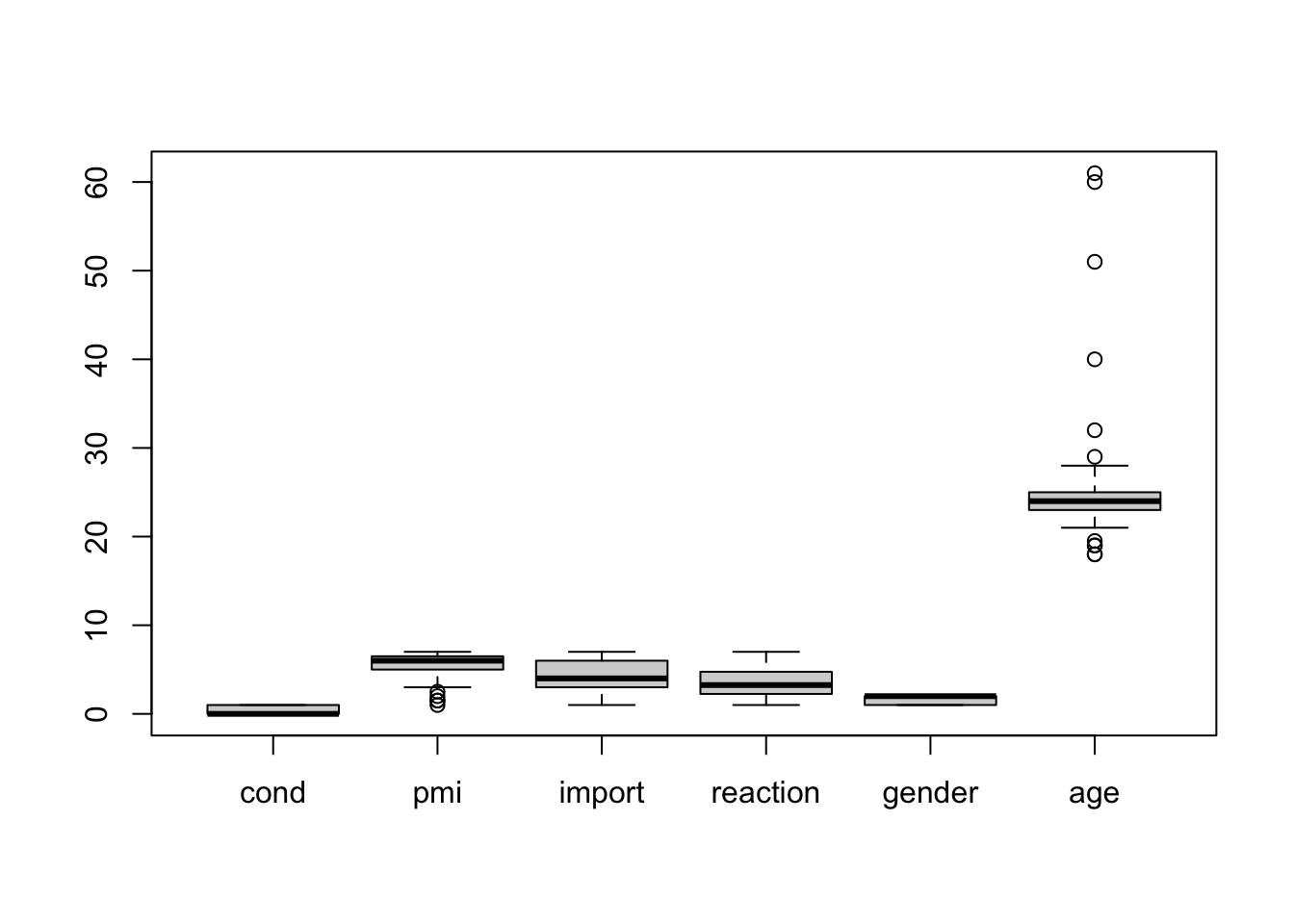
str(media$gender) # gender is a numeric variable## num [1:123] 1 1 1 2 1 1 2 1 1 1 ...
## - attr(*, "value.labels")= Named num [1:2] 1 0
## ..- attr(*, "names")= chr [1:2] "male" "female"media$gender <- factor(media$gender, levels = c(1, 2), labels = c("male", "female"))
str(media$gender)## Factor w/ 2 levels "male","female": 1 1 1 2 1 1 2 1 1 1 ...2. Dummy Coding
Option 1: Manual coding
ให้ male เป็นระดับอ้างอิง (0)
media$genderDum <- ifelse(media$gender == "female", 1, 0)
# if you have more levels
# media$genderDum2 <- ifelse(media$gender == "other", 1, 0)จำนวนตัวแปร dummy = k -1 ถ้ามี 3 ระดับต้องสร้าง 2ตัว ถ้ามี 4 ระดับต้องสร้าง 3 ตัว
Option 2: dummy_cols
แพ็คเกจ fastDummies
เลือก option remove_first_dummy = TRUE
levels(media$gender) #check levels## [1] "male" "female"media <- dummy_cols(media, select_columns = "gender", remove_first_dummy = TRUE)
# dummy varaible name is set to gender_*levelname*, which is gender_female
media[c("gender","genderDum", "gender_female")] # check for errors in dummy coding## gender genderDum gender_female
## 1 male 0 0
## 2 male 0 0
## 3 male 0 0
## 4 female 1 1
## 5 male 0 0
## 6 male 0 0
## 7 female 1 1
## 8 male 0 0
## 9 male 0 0
## 10 male 0 0
## 11 female 1 1
## 12 female 1 1
## 13 female 1 1
## 14 female 1 1
## 15 female 1 1
## 16 female 1 1
## 17 female 1 1
## 18 female 1 1
## 19 female 1 1
## 20 male 0 0
## 21 female 1 1
## 22 female 1 1
## 23 male 0 0
## 24 male 0 0
## 25 female 1 1
## 26 male 0 0
## 27 female 1 1
## 28 female 1 1
## 29 female 1 1
## 30 male 0 0
## 31 female 1 1
## 32 female 1 1
## 33 female 1 1
## 34 female 1 1
## 35 male 0 0
## 36 female 1 1
## 37 male 0 0
## 38 male 0 0
## 39 male 0 0
## 40 male 0 0
## 41 male 0 0
## 42 female 1 1
## 43 male 0 0
## 44 female 1 1
## 45 male 0 0
## 46 male 0 0
## 47 female 1 1
## 48 male 0 0
## 49 male 0 0
## 50 male 0 0
## 51 male 0 0
## 52 male 0 0
## 53 male 0 0
## 54 female 1 1
## 55 male 0 0
## 56 male 0 0
## 57 male 0 0
## 58 female 1 1
## 59 female 1 1
## 60 male 0 0
## 61 female 1 1
## 62 female 1 1
## 63 female 1 1
## 64 female 1 1
## 65 female 1 1
## 66 female 1 1
## 67 male 0 0
## 68 female 1 1
## 69 female 1 1
## 70 female 1 1
## 71 female 1 1
## 72 female 1 1
## 73 male 0 0
## 74 female 1 1
## 75 female 1 1
## 76 female 1 1
## 77 female 1 1
## 78 male 0 0
## 79 female 1 1
## 80 female 1 1
## 81 male 0 0
## 82 male 0 0
## 83 female 1 1
## 84 female 1 1
## 85 male 0 0
## 86 female 1 1
## 87 male 0 0
## 88 female 1 1
## 89 female 1 1
## 90 female 1 1
## 91 female 1 1
## 92 female 1 1
## 93 male 0 0
## 94 female 1 1
## 95 female 1 1
## 96 female 1 1
## 97 female 1 1
## 98 female 1 1
## 99 female 1 1
## 100 female 1 1
## 101 female 1 1
## 102 female 1 1
## 103 female 1 1
## 104 female 1 1
## 105 female 1 1
## 106 female 1 1
## 107 female 1 1
## 108 female 1 1
## 109 male 0 0
## 110 female 1 1
## 111 female 1 1
## 112 female 1 1
## 113 female 1 1
## 114 male 0 0
## 115 female 1 1
## 116 female 1 1
## 117 female 1 1
## 118 male 0 0
## 119 female 1 1
## 120 female 1 1
## 121 female 1 1
## 122 female 1 1
## 123 female 1 13. Step 1: Control variables
Dummy for categorical variables
media1.lm <- lm(reaction ~ genderDum + age, media)
summary(media1.lm)##
## Call:
## lm(formula = reaction ~ genderDum + age, data = media)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.5302 -1.2095 -0.0302 1.2565 3.5875
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.09239 0.73537 5.565 1.62e-07 ***
## genderDum -0.04432 0.31069 -0.143 0.887
## age -0.02354 0.02564 -0.918 0.360
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.558 on 120 degrees of freedom
## Multiple R-squared: 0.007179, Adjusted R-squared: -0.009368
## F-statistic: 0.4338 on 2 and 120 DF, p-value: 0.649Let R codes categorical variables for you
เราสามารถใส่ตัวแปร factor ลงไปในสมการได้เลย R จะทำการ code ให้เราเอง (ในขั้นนี้ต้องระวัง ตัวแปรที่เป็น factor ต้องแปลงเป็น factor ให้เรียบร้อยก่อน)
R แต่ละ version อาจจะมีวิธี code ให้แตกต่างกัน จึงควรกำหนด
contrasts = list(*var_name* = "contr.treatment") เพื่อให้ R
ใช้วิธี dummy code (ref level = 0) ใน R เรียกวิธีนี้ว่า
contr.treatment
media.R.lm <- lm(reaction ~ gender + age, media, contrasts = list(gender = "contr.treatment"))
summary(media.R.lm)##
## Call:
## lm(formula = reaction ~ gender + age, data = media, contrasts = list(gender = "contr.treatment"))
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.5302 -1.2095 -0.0302 1.2565 3.5875
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.09239 0.73537 5.565 1.62e-07 ***
## genderfemale -0.04432 0.31069 -0.143 0.887
## age -0.02354 0.02564 -0.918 0.360
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.558 on 120 degrees of freedom
## Multiple R-squared: 0.007179, Adjusted R-squared: -0.009368
## F-statistic: 0.4338 on 2 and 120 DF, p-value: 0.6494. Step 2: Add predictors
4.1 pmi
# For nonDummy version
# media2.lm <- lm(reaction ~ gender + age + pmi, media,
# contrasts = list(gender = "contr.treatment"))
# For dummy version
media2.lm <- lm(reaction ~ genderDum + age + pmi, data = media)
plot(media2.lm) # scale-location plot suggest heteroscedasticity, perhaps because pmi is negatively skewed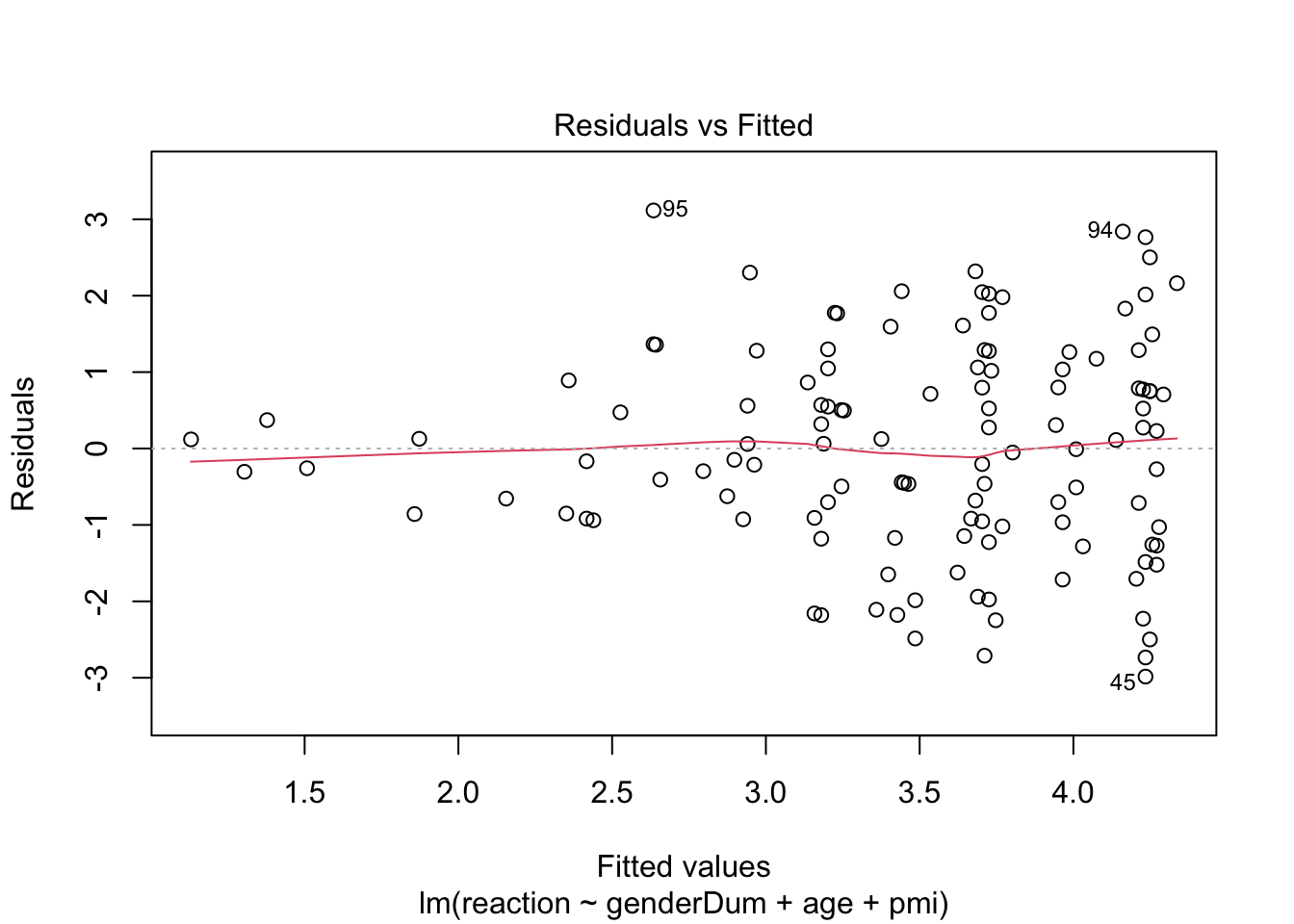
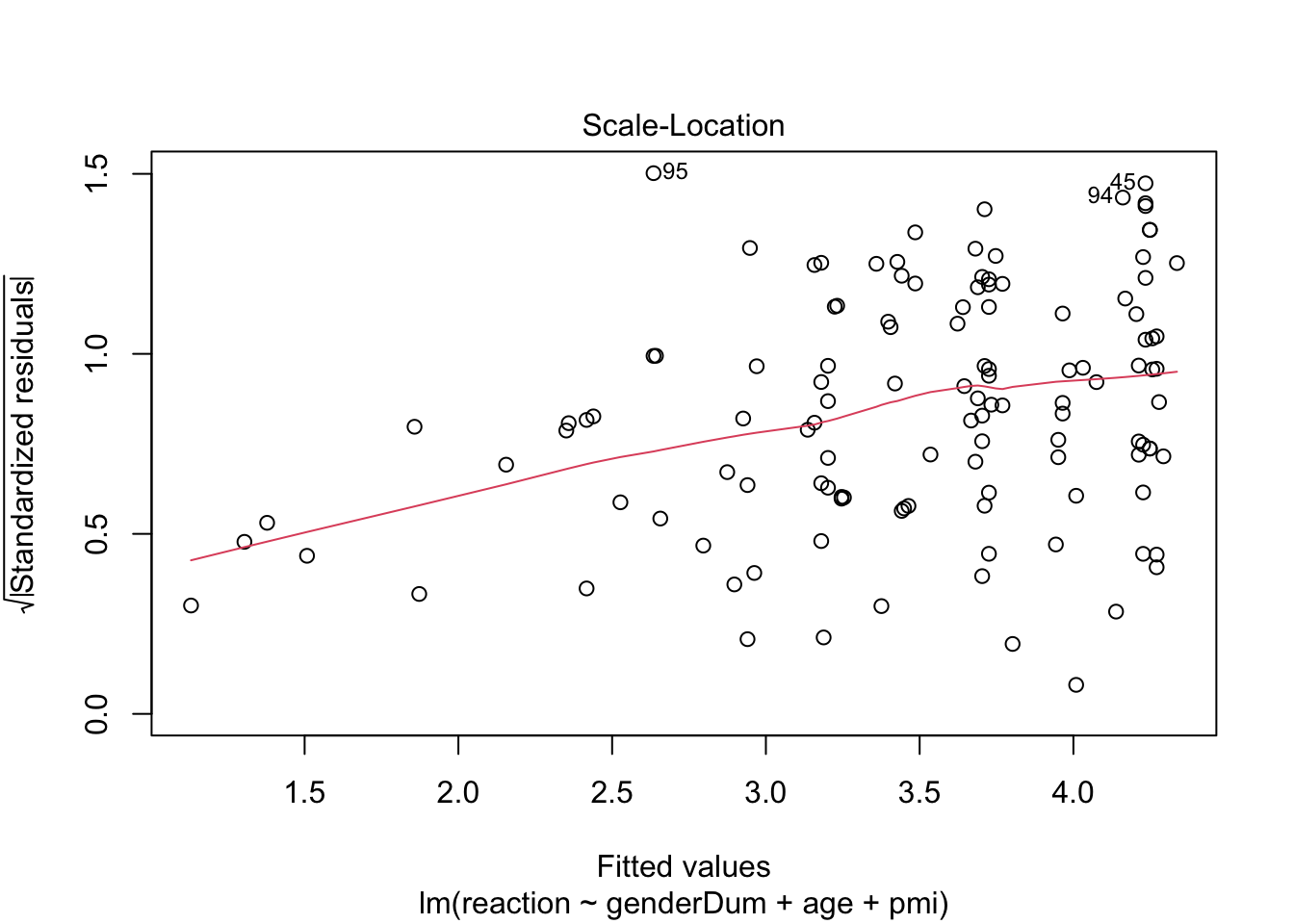
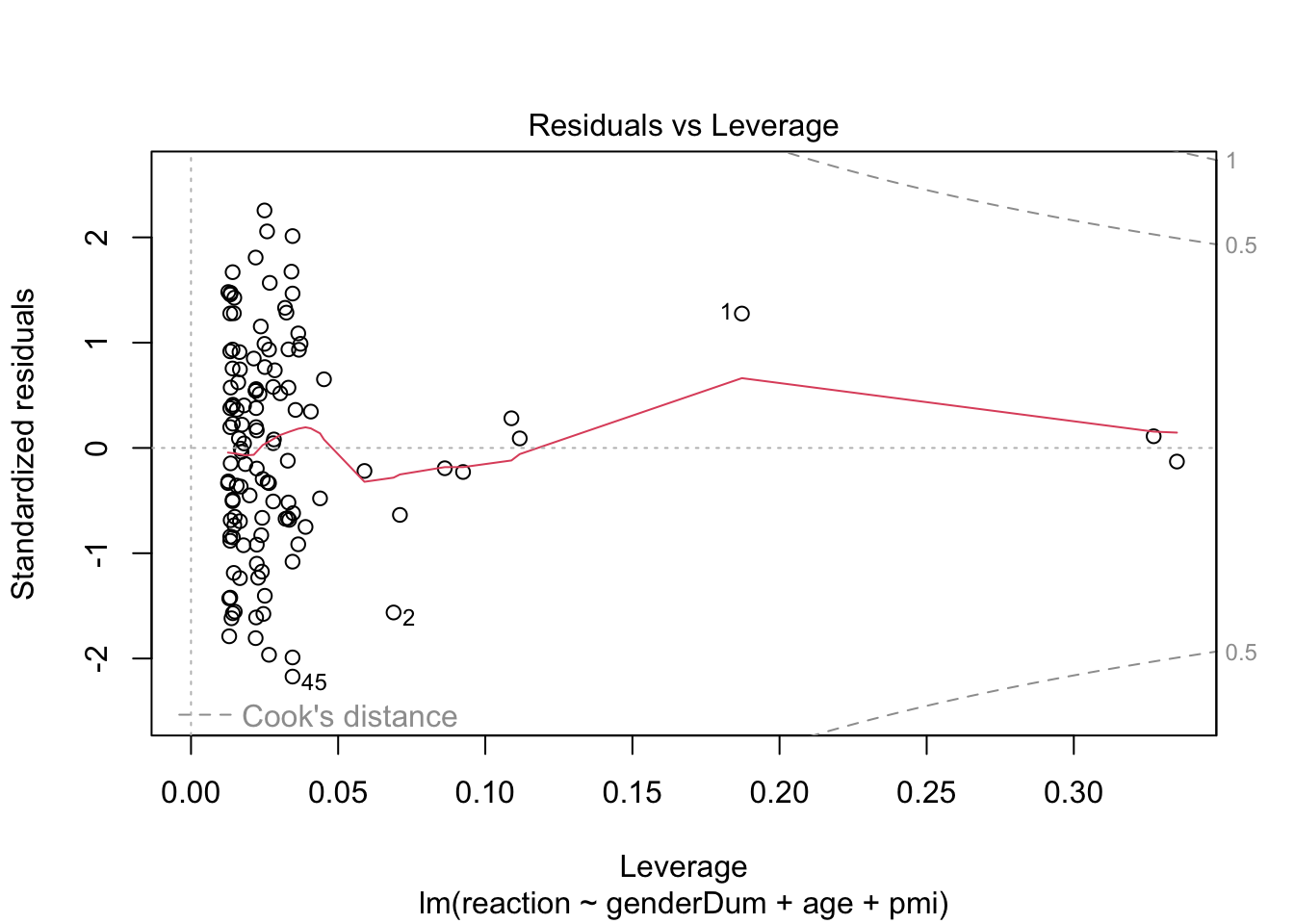
# check influence
influenceIndexPlot(media2.lm) # data seems fine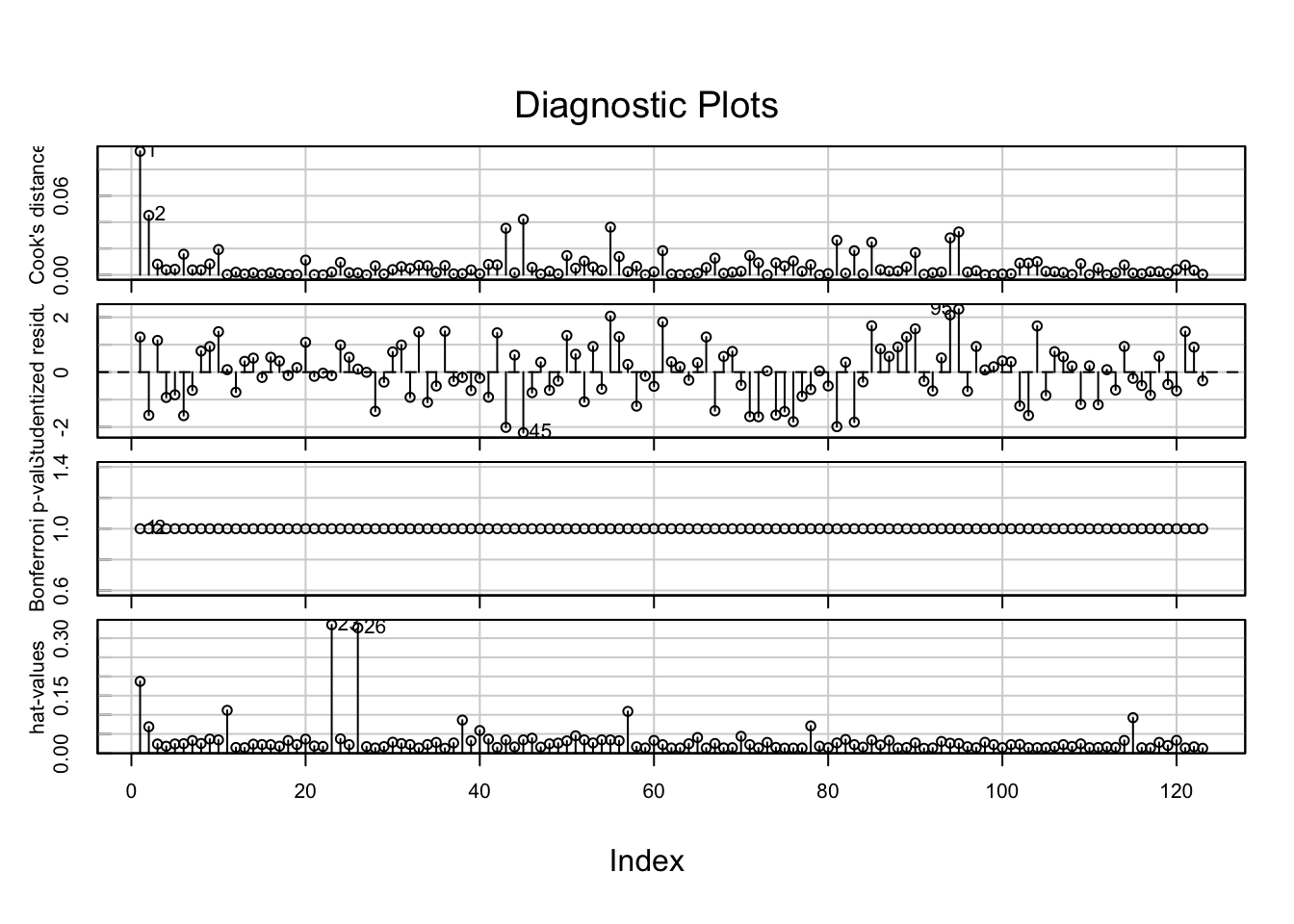
# Show regression output
summary(media2.lm) # notice pmi slope for now##
## Call:
## lm(formula = reaction ~ genderDum + age + pmi, data = media)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.98454 -0.94615 0.05969 1.02590 3.11535
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.098891 0.858382 1.280 0.203
## genderDum -0.007839 0.279092 -0.028 0.978
## age -0.021993 0.023030 -0.955 0.342
## pmi 0.523354 0.095872 5.459 2.66e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.399 on 119 degrees of freedom
## Multiple R-squared: 0.206, Adjusted R-squared: 0.186
## F-statistic: 10.29 on 3 and 119 DF, p-value: 4.484e-06# Compare models
anova(media1.lm , media2.lm)## Analysis of Variance Table
##
## Model 1: reaction ~ genderDum + age
## Model 2: reaction ~ genderDum + age + pmi
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 120 291.11
## 2 119 232.81 1 58.3 29.8 2.657e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 14.2 import
# For nonDummy version
# media3.lm <- lm(reaction ~ gender + age + pmi + import, media,
# contrasts = list(gender = "contr.treatment"))
# For dummy version
media3.lm <- lm(reaction ~ genderDum + age + pmi + import, media)
plot(media3.lm) # some violation of hemoscedasticity, but regression is quite robust.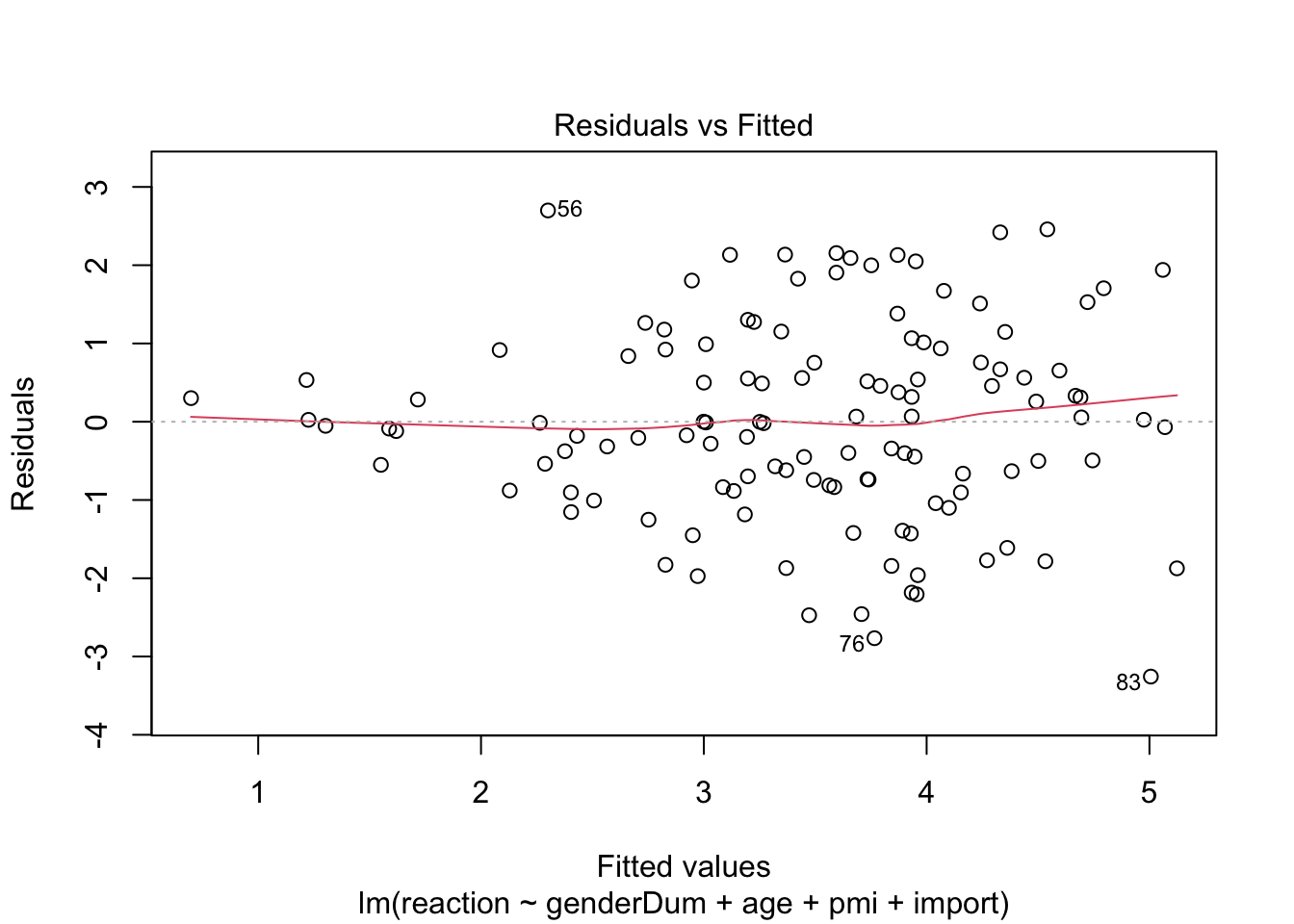
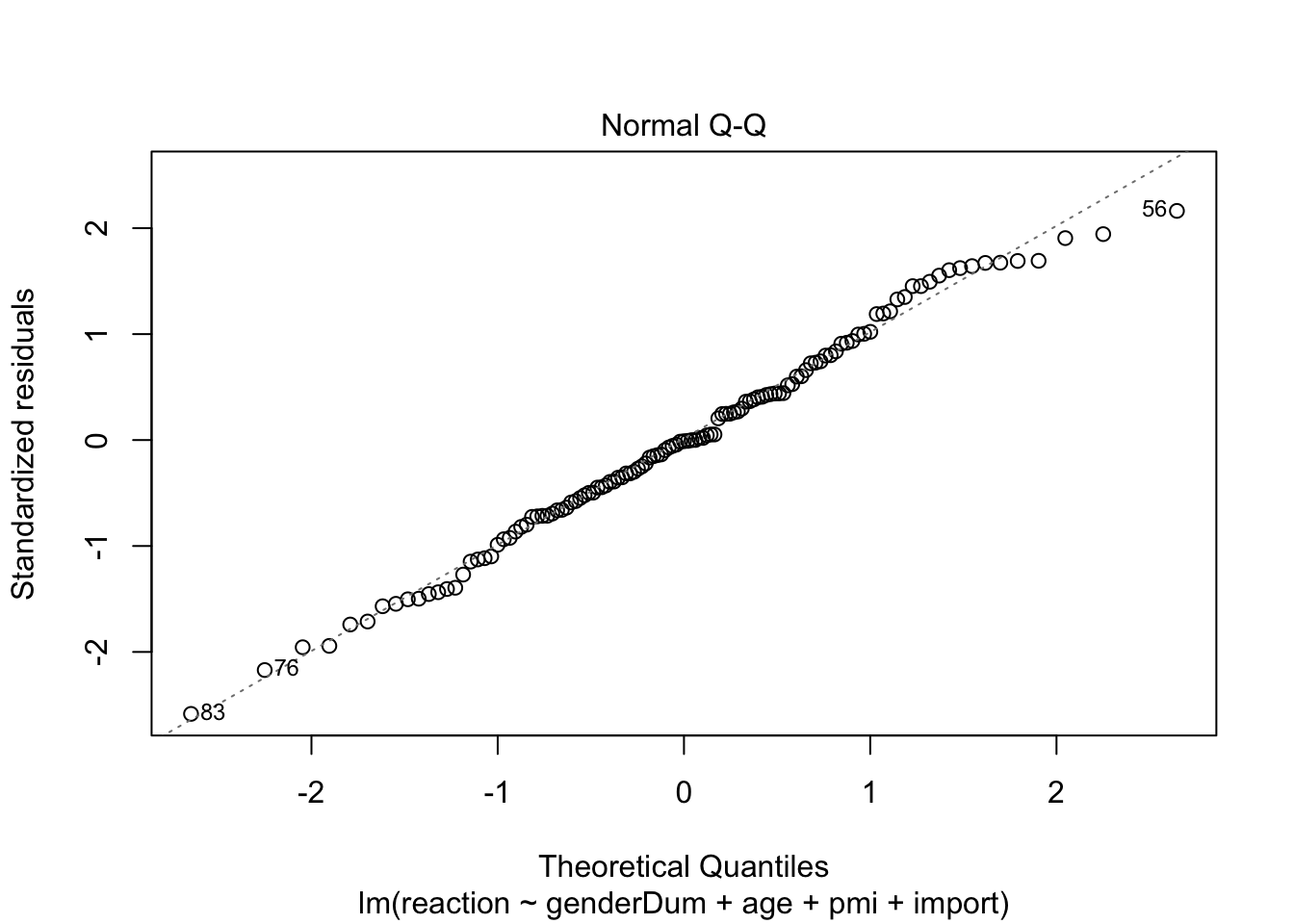
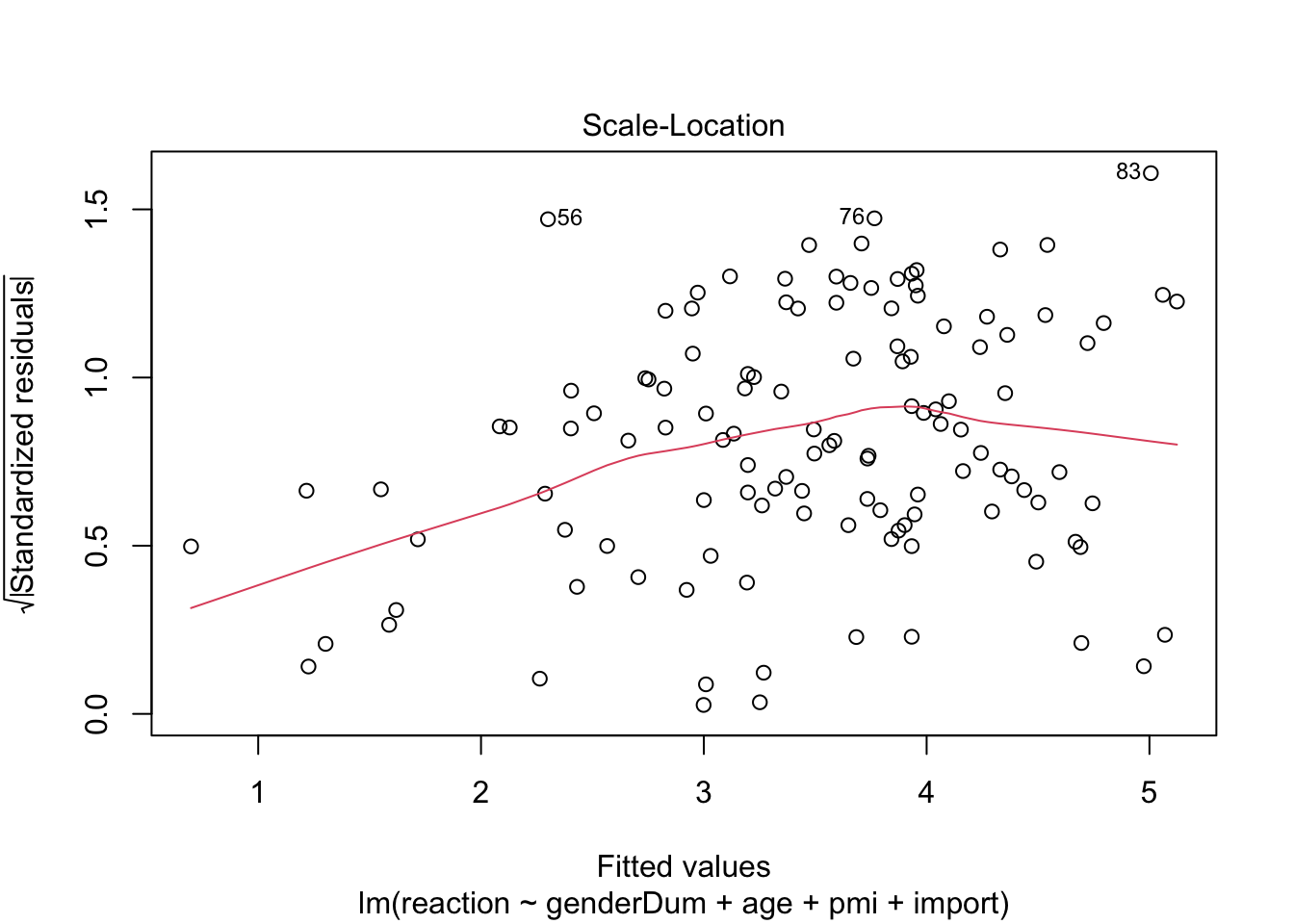
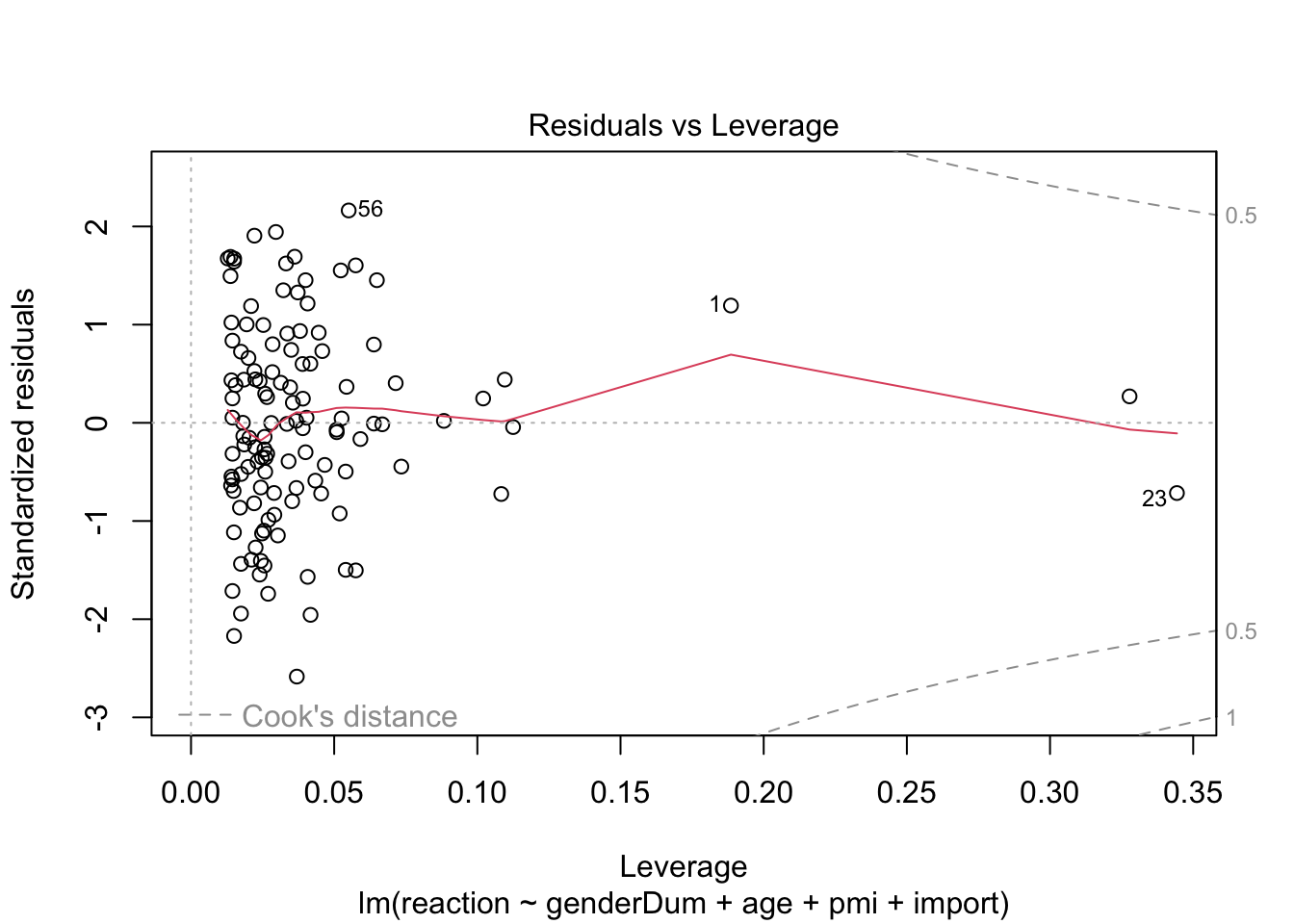
influenceIndexPlot(media3.lm) 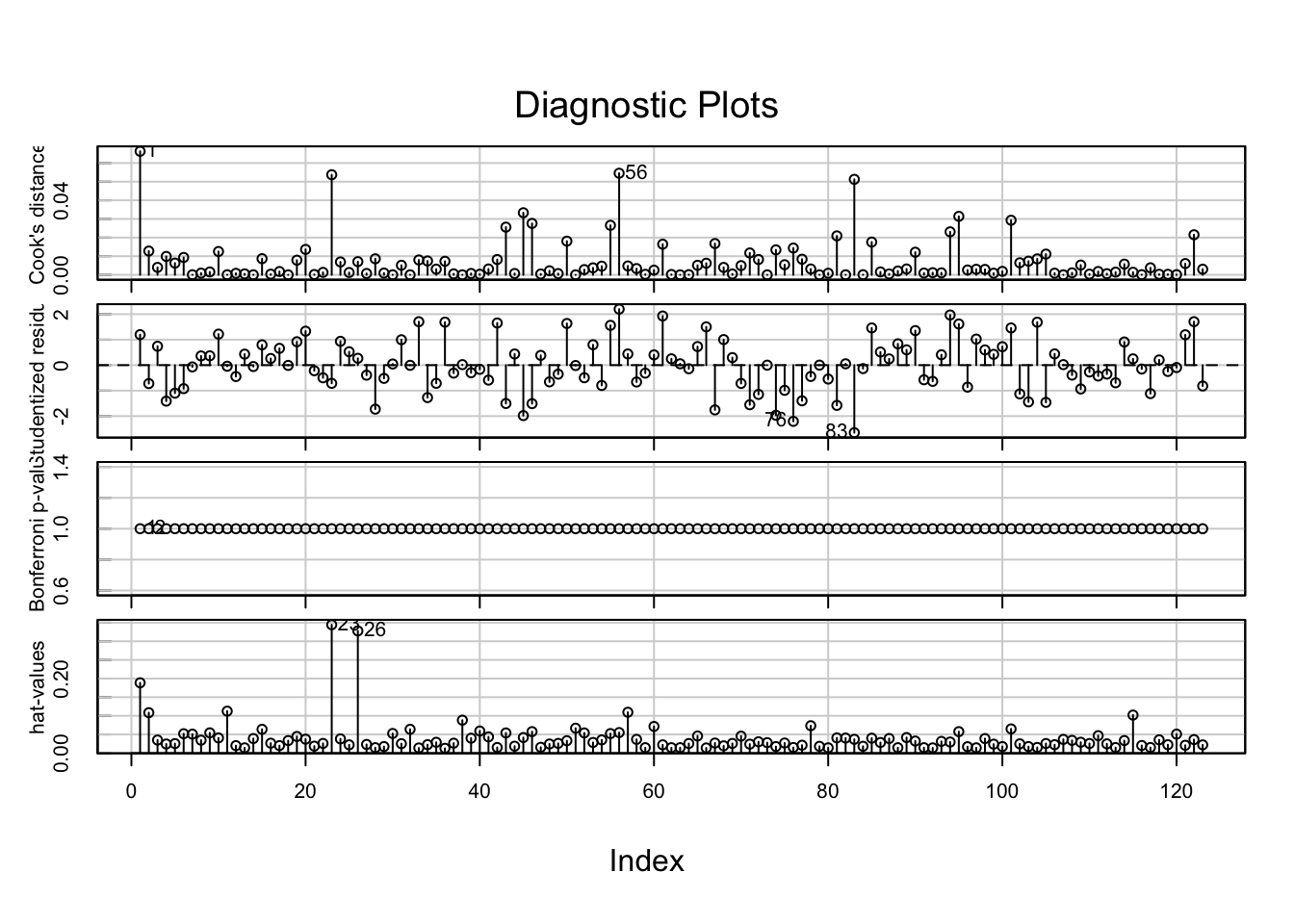
vif(media3.lm) # multi-collinearity seems fine## genderDum age pmi import
## 1.117884 1.122924 1.089033 1.097401summary(media3.lm) # notice change in R-squared and pmi's slope##
## Call:
## lm(formula = reaction ~ genderDum + age + pmi + import, data = media)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.2563 -0.8244 -0.0138 0.8776 2.6995
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.67168 0.79286 0.847 0.399
## genderDum -0.08540 0.25668 -0.333 0.740
## age -0.03160 0.02123 -1.488 0.139
## pmi 0.39722 0.09181 4.327 3.19e-05 ***
## import 0.33806 0.07012 4.821 4.29e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.284 on 118 degrees of freedom
## Multiple R-squared: 0.3367, Adjusted R-squared: 0.3142
## F-statistic: 14.97 on 4 and 118 DF, p-value: 6.325e-10anova(media1.lm, media2.lm, media3.lm) # check if R-squared change was significant## Analysis of Variance Table
##
## Model 1: reaction ~ genderDum + age
## Model 2: reaction ~ genderDum + age + pmi
## Model 3: reaction ~ genderDum + age + pmi + import
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 120 291.11
## 2 119 232.81 1 58.300 35.370 2.848e-08 ***
## 3 118 194.50 1 38.315 23.246 4.292e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Copyright © 2022 Kris Ariyabuddhiphongs