Lab 10: Simple Regression
Mar 30, 2022
# Load packages for this tutorial
library(ggplot2)Model Fitting
การวิเคราะห์ข้อมูลทางสถิตินั้นอาจเรียกได้ว่าเป็นการนำแบบจำลองทางคณิตศาสตร์มาใช้อธิบายข้อมูลเชิงประจักษ์ ยกตัวอย่างเช่น เรามีสมมติฐานว่าบุคลิกภาพแบบ A จะสัมพันธ์ทางบวกกับความดันโลหิต หากเราเชื่อว่าอัตราการเปลี่ยนแปลงความดันโลหิตนั้นคงที่เมื่อบุคลิกภาพแบบ A สูงขึ้นหรือลดลง (เช่น ความดันจะเพิ่มขึ้น 5 มม.ปรอท เมื่อคะแนนบุคลิกภาพเพิ่มขึ้น 1 หน่วยเสมอ) เรากำลังจำลองว่าตัวแปรทั้งสองสัมพันธ์กันเชิงเส้นตรง สามารถเขียนเป็นสมการเส้นตรง \(y = mx + c\) โดยที่ y คือตัวแปรเกณฑ์ (ความดัน) m คือ ความชัน (ค่าที่บอกความสัมพันธ์ระหวางตัวแปร x และ y เช่น 5 มม.ปรอท ในตัวอย่างนี้) x คือตัวแปรทำนาย (ระดับบุคลิกภาพแบบ A) ส่วน c คือ จุดตัดแกน y ที่บอกว่าเส้นตรงนี้จะตัดแกน y (เมื่อ x = 0) ที่จุดไหน
การวิเคราะห์ทางสถิติจำนวนมากตั้งอยู่บนพื้นฐานของสมการเส้นตรง (เช่น t test, correlation, ANOVA, regression) และโปรแกรม R ก็ใช้แนวทางของการสร้างโมเดลเป็นพื้นฐานในการเขียนคำสั่งเช่นกัน
การเขียนโมเดลเส้นตรงให้ตัวแปร x ทำนายตัวแปร y
จะอยู่ในรูปสมการ y ~ x โดยที่ y คือ ตัวแปรตาม/ตัวแปรเกณฑ์
ส่วน x คือตัวแปรอิสระ/ตัวแปรทำนาย
คำสั่งในการ fit โมเดลเส้นตรงเข้ากับข้อมูลคือ
lm(formula = y ~ x, data) โดย y และ
x คือชื่อตัวแปรที่อยู่ใน data คำสั่งนี้จะประมาณค่าพารามิเตอร์
(ค่า slope และ intercept) คำนวณความคลาดเคลื่อนในการทำนาย ผลการทำนาย ฯลฯ
ออกมาเป็น output ที่เราจะเรียกว่า lm object
หลังจากที่เราได้ lm object แล้ว เราจึงค่อยนำมันไปใช้กับคำสั่งอื่น เช่น
summary() plot() confint()
เป็นต้น
ดังนั้นสิ่งที่สำคัญในการวิเคราะห์ข้อมูล คือ
การเลือกโมเดลให้เหมาะสมกับข้อมูลที่เราต้องการจะอธิบาย ยกตัวอย่างด้านล่าง เช่น
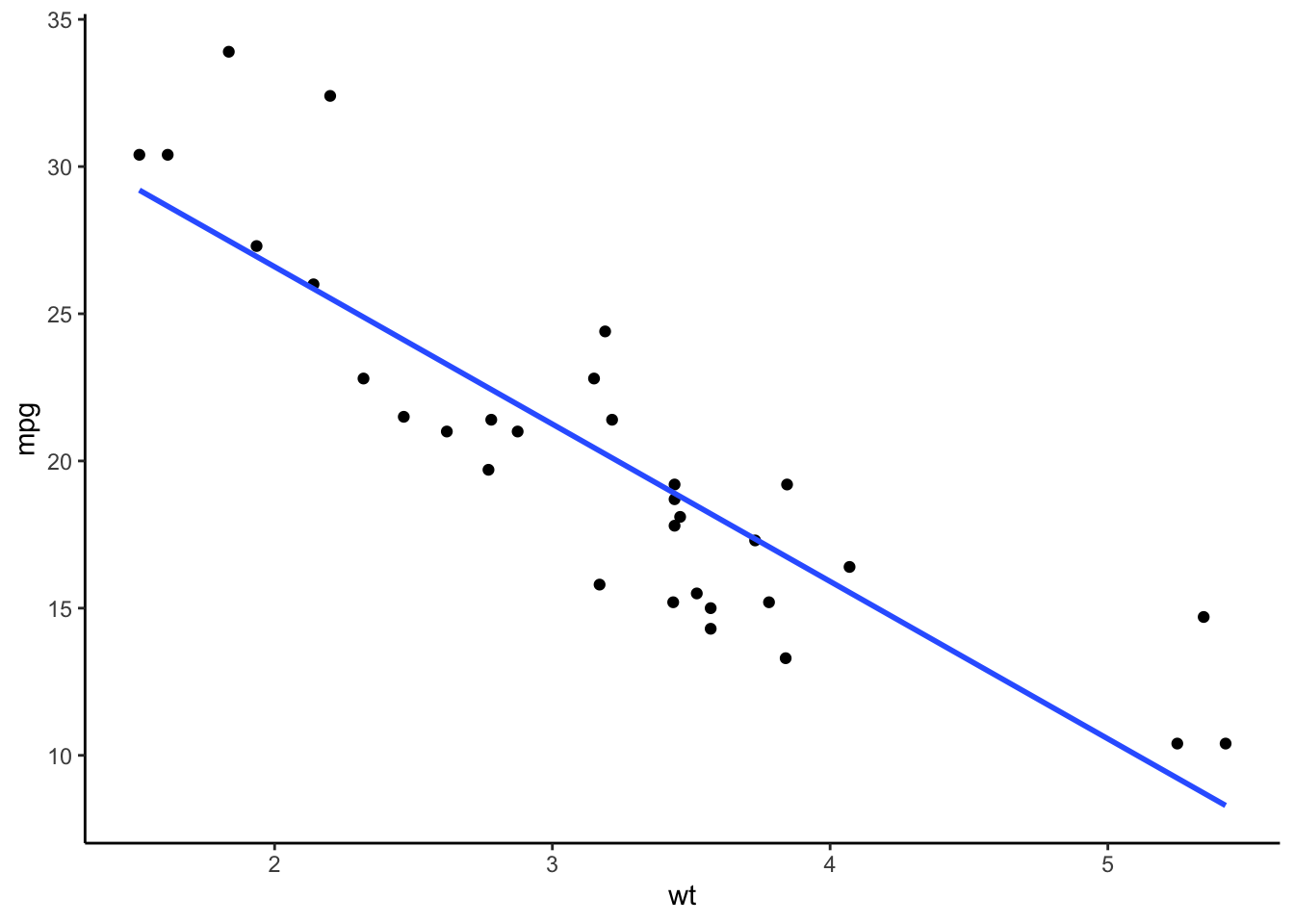
เราต้องการทดสอบว่าน้ำหนักของรถยนต์ wt
สัมพันธ์เชิงเส้นตรงในทางลบกับอัตราประหยัดน้ำมัน mpg
(ยิ่งหนักยิ่งประหยัดน้อย) หรือไม่
Simple Regression
สำหรับการวิเคราะห์ถดถอยอย่างง่าย (simple regression analysis) เราจะทดสอบความสัมพันธ์เชิงเส้นตรงระหว่างตัวแปรทำนาย (X) และตัวแปรเกณฑ์ (Y)
การ fit โมเดลเส้นตรง ทำโดยใช้คำสั่ง lm(formula, data) โดย
formula
เป็นโมเดลทางสถิติที่บอกว่าตัวแปรใดเป็นตัวแปรทำนายตัวแปรใดเป็นตัวแปรเกณฑ์ ส่วน
data คือ data frame
ในตัวอย่างนี้เราจะใช้ชุดข้อมูล mtcars ซึ่งเป็นข้อมูลเกี่ยวกับรถยนต์รุ่นต่าง
ๆ โดยเราต้องการทำนายอัตราการประหยัดน้ำมัน mpg
ด้วยตัวแปรน้ำหนักของรถยนต์ wt
data(mtcars) #load dataset
head(mtcars) #show first 6 rows## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1ในโปรแกรม R เราจะเขียนสมการในรูปแบบ y ~ x ดังนั้นสมการ
(formula) ของตัวอย่างนี้คือ mpg ~ wt
(ใช้นำ้หนักทำนายอัตราประหยัดน้ำมัน)
เมื่อเรา fit โมเดลนี้ด้วยคำสั่ง lm() เราจะบันทึกผลเป็น object
ที่ชื่อว่า reg.lm ใน object นี้จะมีข้อมูลที่สำคัญเกี่ยวกับการวิเคราะห์
regression
ในเบื้องต้นเราจะใช้คำสั่ง summary() เพื่อดู output
ของการวิเคราะห์ถดถอย และใช้คำสั่ง confint() เพื่อดู 95% CI
ของค่าประมาณการพารามิเตอร์ในโมเดล (เช่น ค่า intercept และ slope)
reg.lm <- lm(mpg ~ wt, mtcars)
summary(reg.lm)##
## Call:
## lm(formula = mpg ~ wt, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5432 -2.3647 -0.1252 1.4096 6.8727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.2851 1.8776 19.858 < 2e-16 ***
## wt -5.3445 0.5591 -9.559 1.29e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.046 on 30 degrees of freedom
## Multiple R-squared: 0.7528, Adjusted R-squared: 0.7446
## F-statistic: 91.38 on 1 and 30 DF, p-value: 1.294e-10confint(reg.lm)## 2.5 % 97.5 %
## (Intercept) 33.450500 41.119753
## wt -6.486308 -4.202635R Output
ส่วน Call: แสดงสูตรโมเดลที่เรากำลังวิเคราะห์
ส่วน Residuals: แสดงความคลาดเคลื่อนในการทำนาย, \(Y-\hat{Y}\).
ส่วน Coefficients: แสดงค่าสัมประสิทธิ์ในสมการเส้นตรง ได้แก่
ค่าจุดตัดแกน Y (intercept) และความชัน (slope) ของตัวแปรทำนาย
รวมไปถึงการทดสอบนัยสำคัญทางสถิติของค่าแต่ละตัว
เครื่องหมายดอกจัน (asterisks [*]) เป็นตัวบอกระดับนัยสำคัญทางสถิติที่ระดับ \(\alpha\) ต่าง ๆ กัน
ส่วนต่อไปแบ่งได้เป็นดังนี้
Residual standard errorคือ ค่าความคลาดเคลื่อนมาตรฐานของ residualsdegrees of freedomคือ df ของ residual = \(N-k-1\) (k = number of parameters)Multiple R-squared(\(R^2\)) คือ สัดส่วนความแปรปรวนใน Y ที่อธิบายได้ด้วย X (variance explained)Adjusted R-squaredคือค่า \(R^2\) ที่ปรับแก้จำนวนตัวแปรทำนายแล้วเพื่อให้แม่นยำมากขึ้น (สำหรับ simple regression ที่มีตัวแปรทำนายเพียงตัวเดียว ค่านี้มักใกล้เคียงกับ un-adjusted \(R^2\) )F-statisticเป็นการทดสอบโมเดลในภาพรวม ใน simple regression ผลการทดสอบค่า F นี้จะสอดคล้องกับการทดสอบค่า slopeDFตัวแรกเป็น df ของ regression model = \(k\) (จำนวนสัมประสิทธิ์ของตัวแปรทำนาย) และตัวที่สองเป็น df ของ residuals (\(N-k-1\))p-valueของสถิติ F
Coefficients
ในการวิเคราะห์นี้ เราสามารถนำค่าสัมประสิทธิ์มาเขียนเป็นสมการทำนายได้เป็น \(\hat{Y}_{mpg} = 37.285 - 5.344X_{wt}\)
โดยดูค่า intercept และ slope จาก summary()
จุดตัดแกน Y (intercept, \(b_0\)) เป็นค่าทำนายตัวแปร Y เมื่อ X = 0 ในตัวอย่างนี้ อัตราประหยัดน้ำมันของรถที่มีนำ้หนัก 0 ตัน คือ 37.29 ไมล์ต่อแกลลอน เราจะสังเกตได้ว่าค่าจุด intercept นี้ไม่ใช่ค่าที่เราสนใจ เพราะเราไม่ได้ต้องการรู้ว่ารถน้ำหนัก 0 ตันจะมีอัตราประหยัดน้ำมันเท่าใด (แต่อาจจะเป็นค่าที่เราสนใจในกรณีอื่น เช่น คนที่ได้รับยา 0 mg จะมีผลเช่นไร)
ค่าที่เราสนใจคือ สัมประสิทธิ์ที่แสดงถึงความสัมพันธ์ระหว่าง
wtและmpgนั่นก็คือ ค่าความชันของตัวแปรwt, b = -5.34 ค่าทางลบแสดงว่าเมื่อน้ำหนักรถเปลี่ยนแปลงไปหนึ่งตัน อัตราประหยัดน้ำมันจะเปลี่ยนไปในทิศทางตรงกันข้าม 5.34 ไมล์ต่อแกลลอน
reg.lm$coefficients## (Intercept) wt
## 37.285126 -5.344472Hypothesis testing
สถิติทดสอบ t ของค่าสัมประสิทธิ์แต่ละตัวมีสมมติฐานว่าง \(H_0: b = 0\) จึงเป็นการทดสอบว่าค่า b แต่ละตัวแตกต่างจาก 0 อย่างมีนัยสำคัญทางสถิติหรือไม่ นั่นคือ ตัวแปร X มีความสัมพันธ์(ทางบวกหรือทางลบ) กับตัวแปร Y หรือไม่ (แค่บอกว่าค่าความสัมพันธ์นี้อาจแตกต่างจาก 0 แต่ยังไม่ได้บอกว่าสัมพันธ์กันมากหรือน้อย ซึ่งต้องไปดูที่ค่า \(R^2\))
ค่าทดสอบ t ได้มาจากการนำค่า Estimate (intercept or
slope) มาหารด้วย Std. Error(SE) จากนั้นนำค่า
t ที่ได้ไปเทียบกับการแจกแจงของสถิติ t เพื่อดูว่าถึงระดับนัยสำคัญหรือไม่
(ในโปรแกรม สามารถดูที่ค่า p value ได้เลย)
ค่า p เป็นความน่าจะเป็นที่จะพบค่าสัมประสิทธิ์ (b) ขนาดที่ได้หรือมากกว่า หากสมมติฐานว่างเป็นจริง (ไม่มีความสัมพันธ์กันในระดับประชากร) ค่า p ที่น้อยกว่า .05 แสดงว่า เรามีโอกาสน้อยมากที่จะเจอค่าสัมประสิทธิ์ขนาดนี้ หากจริง ๆ แล้วตัวแปรไม่สัมพันธ์กัน เราจึงอนุมานว่ามีความสัมพันธ์นี้อยู่จริง เราจึงอาจะสรุปได้ว่าค่าสัมประสิทธิ์ที่มีนัยสำคัญทางสถิติ อาจจะแตกต่างจาก 0 (may no be zero)
Confidence interval of coefficients
เราสามารถหาช่วงความเชื่อมั่น 95% ของค่าสัมประสิทธิ์แต่ละตัวเพื่อดูความคลาดเคลื่อนของการประมาณค่า โดยปกติแล้วค่า 95% CI นี้จะสอดคล้องกับการทดสอบนัยสำคัญทางสถิติ นั่นคือ หากค่าช่วงความเชื่อมั่นไม่ครอบคลุม 0 เราจะพบว่าสัมประสิทธิ์ตัวนั้นมีนัยสำคัญทางสถิติ (อาจจะต่างจาก 0)
แต่ข้อดีของช่วงความเชื่อมั่นคือ มันช่วยให้เราเห็นภาพชัดเจนขึ้นว่าความสัมพันธ์นี้คลาดเคลื่อนได้มากน้อยเพียงใดโดยดูจากความกว้างของช่วงความเชื่อมั่น สำหรับตัวแปรที่อยู่ในหน่วยเดียวกันและมีระดับความเชื่อมั่น 95% เท่ากัน ช่วงที่แคบกว่าจะแสดงถึงความคลาดเคลื่อนที่น้อยกว่า
confint(reg.lm) #default setting is 95% CI## 2.5 % 97.5 %
## (Intercept) 33.450500 41.119753
## wt -6.486308 -4.202635confint(reg.lm, level = .99) # set to 99% CI## 0.5 % 99.5 %
## (Intercept) 32.121659 42.448593
## wt -6.881997 -3.806946ถ้าเราขยับช่วงความเชื่อมั่นขึ้นเป็น 99% เราจะพบว่าช่วงความเชื่อมั่นจะกว้างขึ้นกว่า 95% ที่เป็นเช่นนี้เพราะเราต้องการมั่นใจได้มากขึ้นว่า ช่วงที่เราสร้างจะครอบคลุมค่าเฉลี่ยที่แท้จริงของประชากร จึงต้องใช้ช่วงที่กว้างขึ้นเพื่อเพิ่มโอกาสนั่นเอง
ในตัวอย่างนี้ เราพบว่าช่วงความเชื่อมั่นของ wt ที่ระดับ 99%
ก็ยังไม่ครอบคลุมศูนย์ (ซึ่งก็ตรงกับค่า p ที่น้อยกว่า .01) อยู่ระหว่าง [-6.88,
-3.81 ทำให้เราเชื่อว่า
ค่าความสัมพันธ์ในระดับประชากรน่าจะอยู่ในช่วงดังกล่าว
Standardized coefficients
ค่าสัมประสิทธ์การถดถอยนั้นอยู่ในหน่วยของ Y ที่เปลี่ยนไปตาม 1 หน่วยของ X ทำให้เราไม่สามารถบอกขนาดของความสัมพันธ์จากค่า b ได้โดยตรง ดังนั้นนักวิจัยบางกลุ่มจึงนิยมคำนวณค่าสัมประสิทธิ์มาตรฐาน (standardized coefficients) แทน
ค่า standardized coefficients คำนวณโดยนำ X และ Y
ไปแปลงเป็นคะแนนมาตรฐาน (standard scores; z scores) ด้วยคำสั่ง
scale() แล้วนำมาวิเคราะห์ regression
ค่าสัมประสิทธิ์มาตรฐานหมายความว่า หาก X เปลี่ยนไป 1 SD ค่า Y จะเปลี่ยนไปกี่ SD ทำให้เราสามารถเปรียบเทียบขนาดความสัมพันธ์สัมพัทธ์ (relative strength) กับตัวแปรอื่น ๆ ในโมเดลได้ (ในกรณีของ multiple regression) ค่า standardized coefficients นี้มีชื่อเรียกต่างกันไปตามโปรแกรมสถิติ เช่น beta (\(\beta\)), \(b^*\), \(\tilde{b}\)
std.lm <- lm(scale(mpg) ~ scale(wt), mtcars)
summary(std.lm)##
## Call:
## lm(formula = scale(mpg) ~ scale(wt), data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.75381 -0.39236 -0.02077 0.23388 1.14033
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.040e-15 8.934e-02 0.000 1
## scale(wt) -8.677e-01 9.077e-02 -9.559 1.29e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5054 on 30 degrees of freedom
## Multiple R-squared: 0.7528, Adjusted R-squared: 0.7446
## F-statistic: 91.38 on 1 and 30 DF, p-value: 1.294e-10ค่า intercept สำหรับ standardized coefficient = 0 เสมอ และค่า \(b_{wt}\) =-0.87
สำหรับ simple regression เท่านั้น ค่า std. coefficient นี้จะเท่ากับค่า correlation ด้วย
cor(mtcars$mpg, mtcars$wt)## [1] -0.8676594Prediction
เราสามารถใช้สมการนี้ทำนายค่า mpg สำหรับค่า wt
ที่เราต้องการได้ เช่น หากมีรถที่หนัก 1.5 ตัน เราจะทำนายว่ารถคันนี้มีอัตราประหยัดน้ำมัน
\[ \begin{aligned}
\hat{Y}_{mpg} &= 37.285 - 5.344(1.5) \\
&= 37.285 - 8.016 \\
&= 29.269
\end{aligned} \]
เราสามารถใช้คำสั่ง predict(object, newdata) ได้ โดยที่ newdata
จะต้องเป็น data frame ที่มีตัวแปรชื่อตรงกับตัวแปรทำนายในโมเดล
predict(reg.lm, data.frame(wt = 1.5)) # newdata is a data frame with same variable name. ## 1
## 29.26842predict(reg.lm, data.frame(wt = c(1.0, 1.2, 1.4, 1.6))) # predict multiple new values## 1 2 3 4
## 31.94065 30.87176 29.80287 28.73397predict(reg.lm) # omit newdata to show predicted value for current dataset## Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive Hornet Sportabout
## 23.282611 21.919770 24.885952 20.102650 18.900144
## Valiant Duster 360 Merc 240D Merc 230 Merc 280
## 18.793255 18.205363 20.236262 20.450041 18.900144
## Merc 280C Merc 450SE Merc 450SL Merc 450SLC Cadillac Fleetwood
## 18.900144 15.533127 17.350247 17.083024 9.226650
## Lincoln Continental Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla
## 8.296712 8.718926 25.527289 28.653805 27.478021
## Toyota Corona Dodge Challenger AMC Javelin Camaro Z28 Pontiac Firebird
## 24.111004 18.472586 18.926866 16.762355 16.735633
## Fiat X1-9 Porsche 914-2 Lotus Europa Ford Pantera L Ferrari Dino
## 26.943574 25.847957 29.198941 20.343151 22.480940
## Maserati Bora Volvo 142E
## 18.205363 22.427495Diagnostic Plot
เราสามารถตรวจสอบ assumptions ต่าง ๆ ของ regression ได้ด้วยคำสั่ง
plot()
คำสั่งนี้จะให้กราฟ 4 รูป
Residuals vs Fitted แสดงความสัมพันธ์ระหว่างค่า residual (\(Y-\hat{Y}\)) กับค่า \(\hat{Y}\) ใช้ทดสอบ linearity assumption หากตัวแปรสัมพันธ์เป็นเส้นตรง เส้นสีแดงจะราบตามแกน Y
Normal Q-Q ใช้ตรวจสอบ normality of residuals ถ้าความคลาดเคลื่อนกระจายตัวอย่างเป็นปกติ ค่าจะเรียงตัวอยู่บนเส้นแทยง
Scale-Location หรือ Spread-Location ใช้ตรวจสอบ homoscedasticity เพื่อดูว่าความแปรปรวนของตัวแปร Y เท่ากับในทุกระดับของตัวแปร X หรือไม่ กราฟนี้ควรได้เส้นตรงสีแดง และจุดต่าง ๆ กระจายตัวเท่า ๆ กันทั้งข้างบนและข้างล่างในทุกช่วงของ Fitted values
Residuals vs Leverage ไว้ตรวจสอบค่า leverage และ influence ในโมเดล ค่านี้ควรจะเกาะกลุ่มกันอยู่ในช่วงต้น ๆ ของแกน X เส้นสีแดงควรเป็นเส้นตรง และจุดต่าง ๆ อยู่ห่างจากเส้นประสีแดง (Cook’s distance)
plot(reg.lm)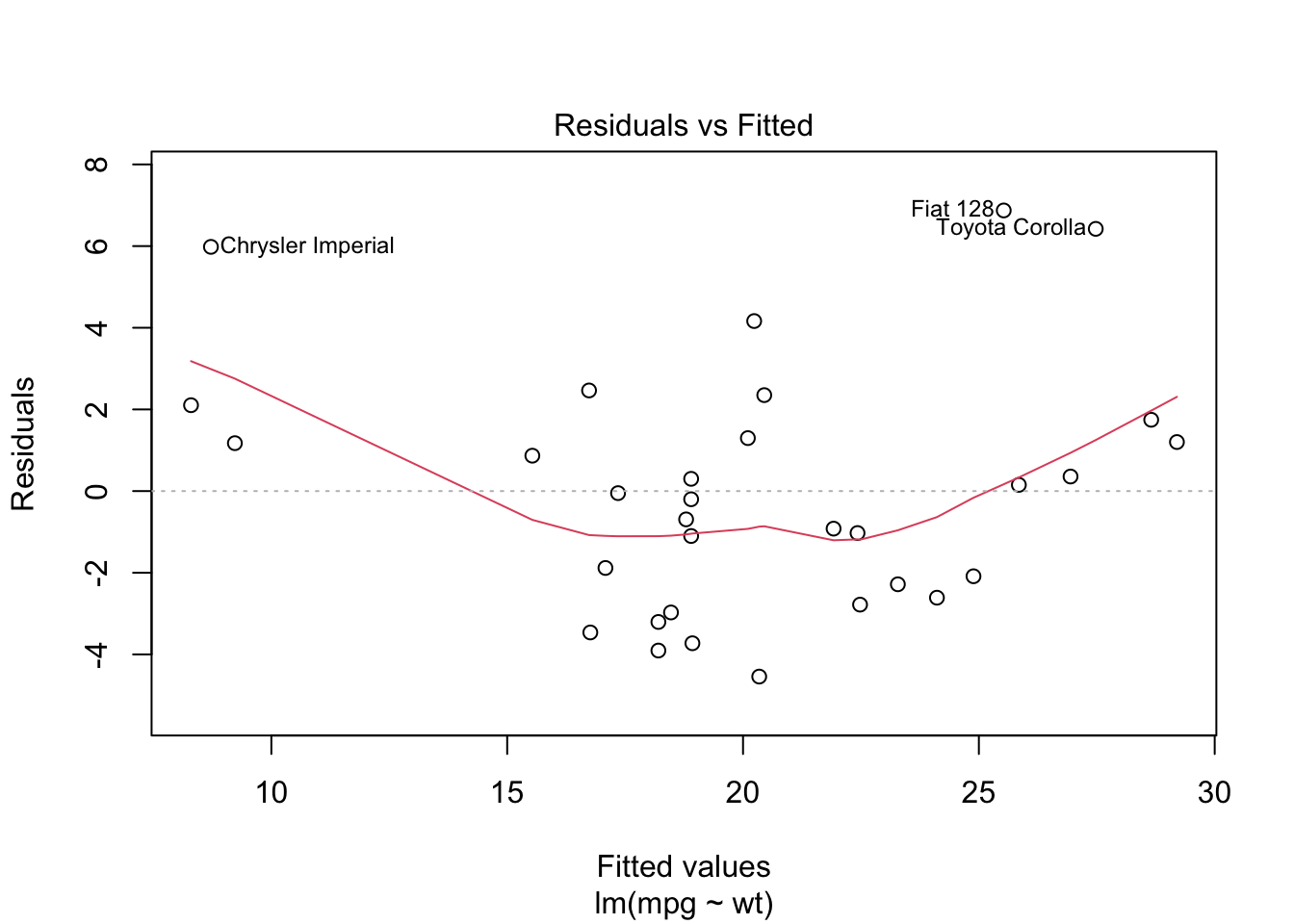
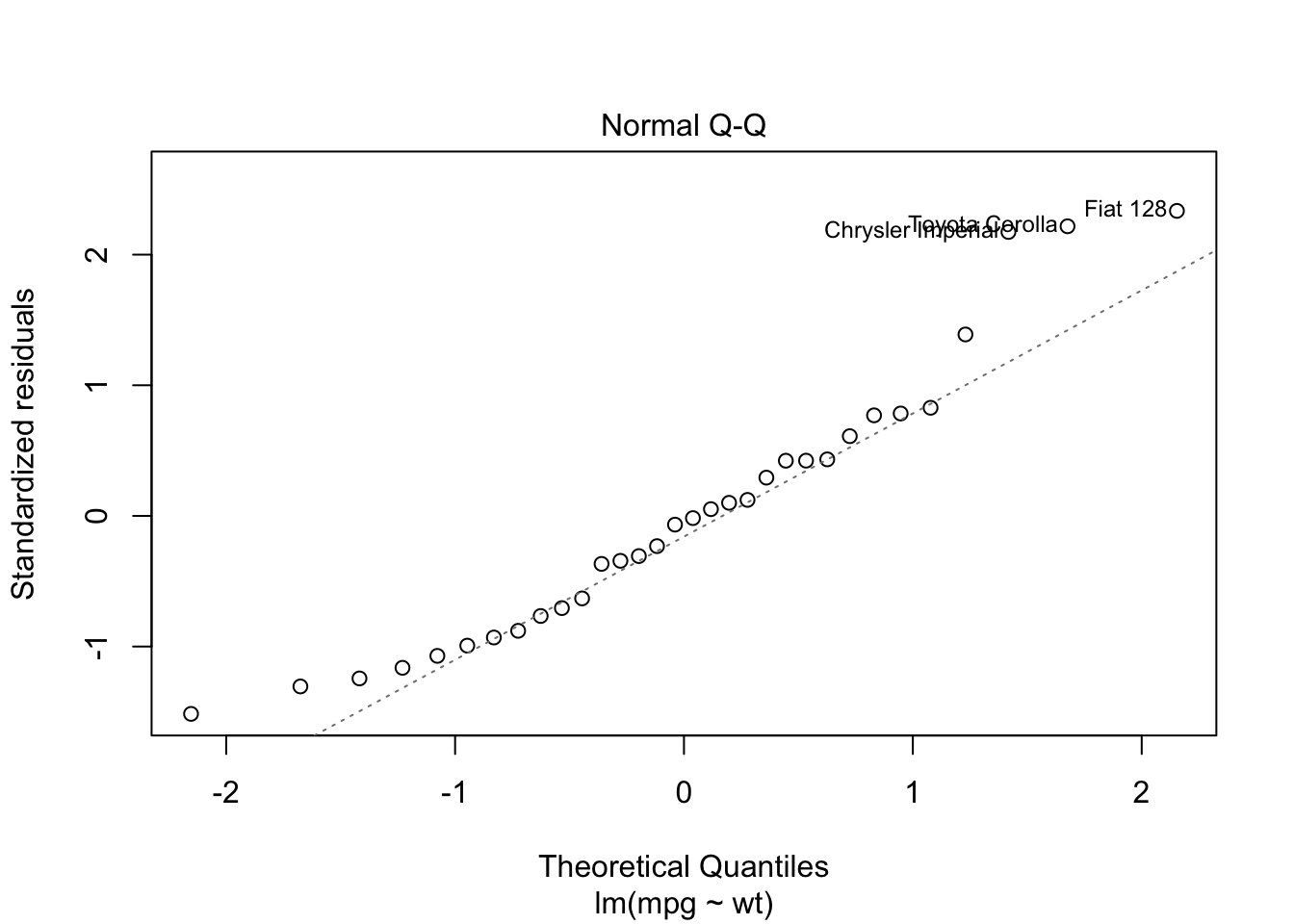
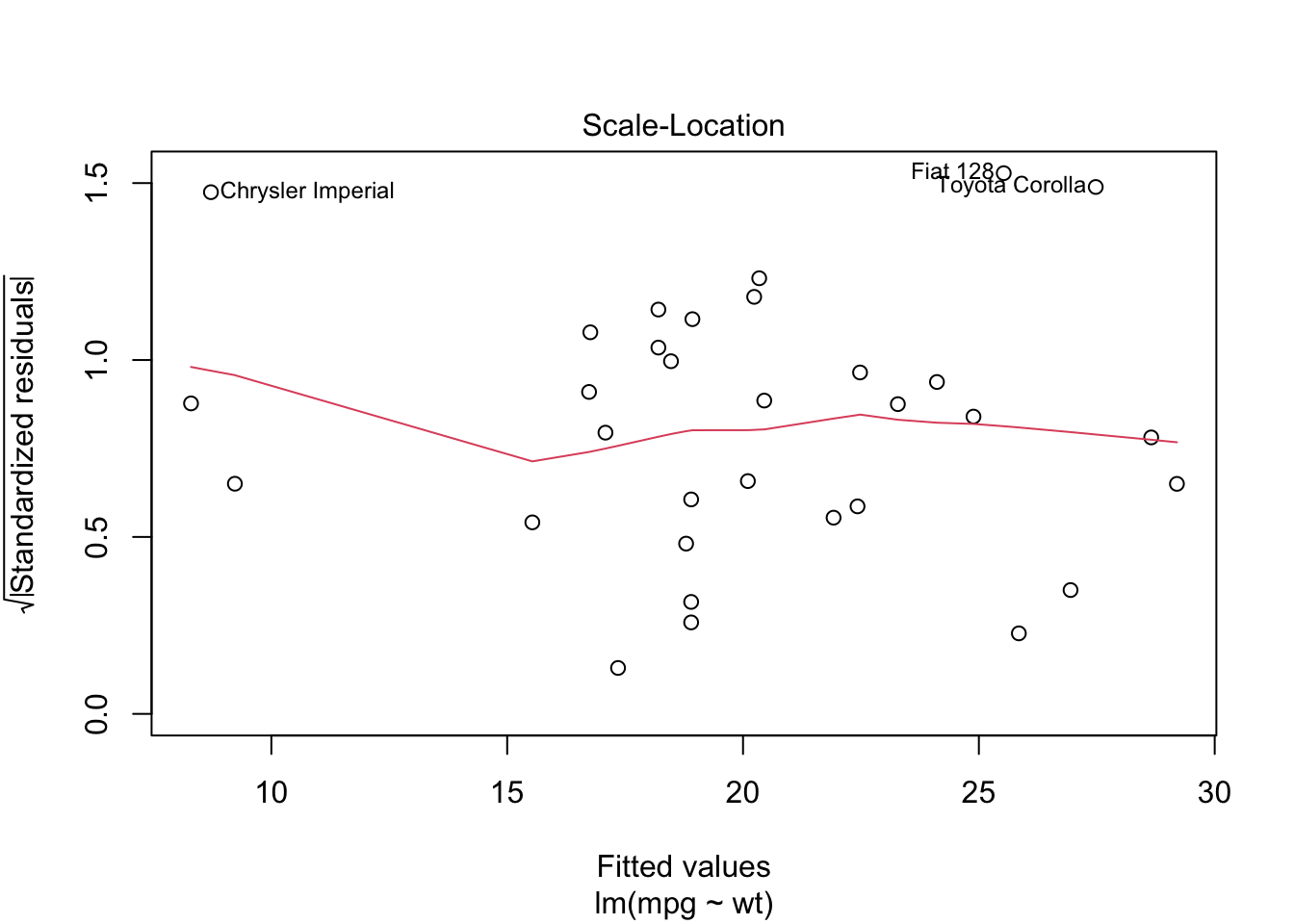
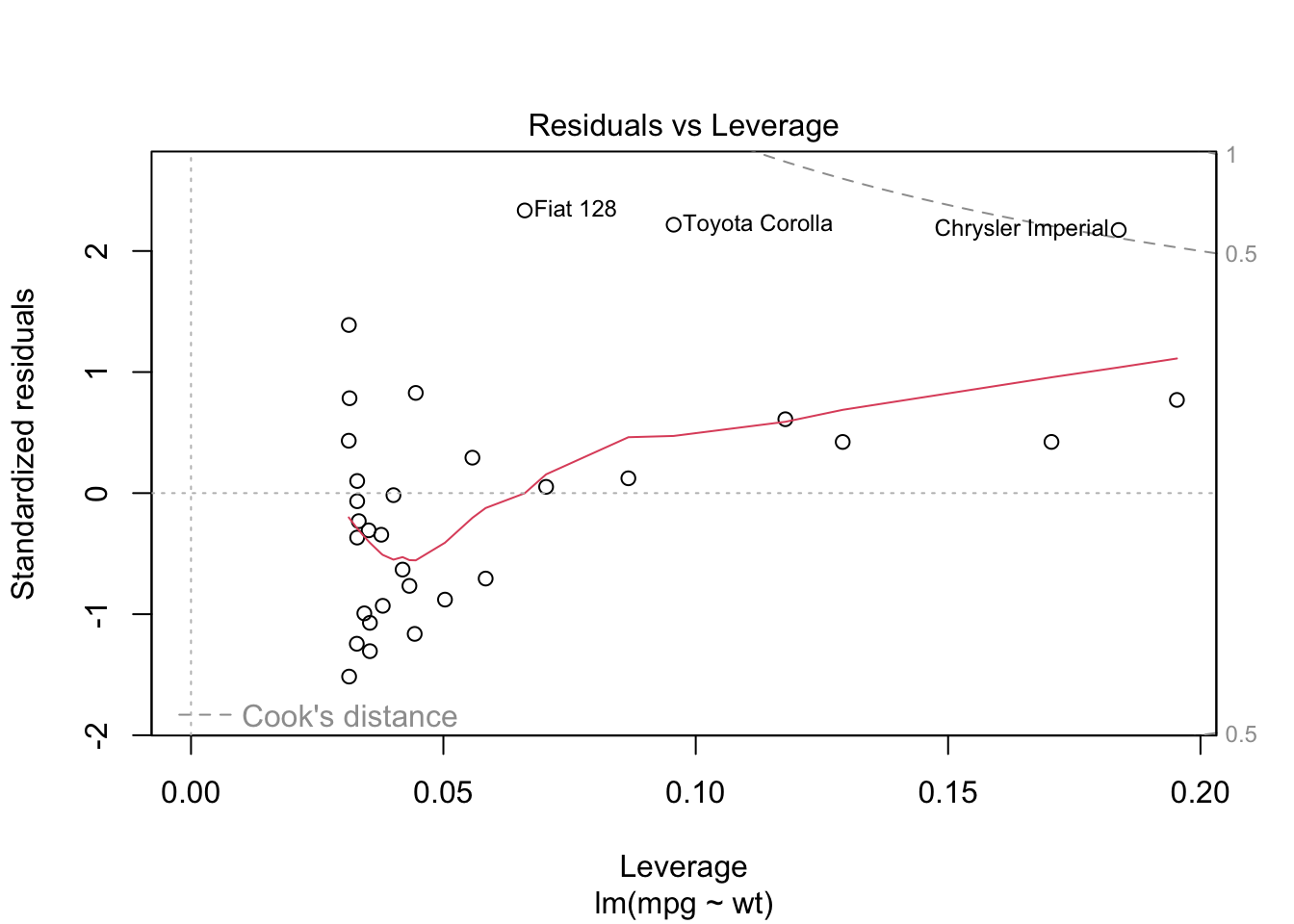
จะเห็นได้ว่าในโมเดลนี้ plot ต่าง ๆ ยังไม่เป็นไปตาม assumption ทั้งหมด อย่างไรก็ดี
regression มีความแกร่งต่อการละเมิดข้อสมมติเบื้องต้นอยู่พอสมควร แม้ข้อมูลจะไม่ตรงตาม
assumption ไปบ้าง แต่ข้อสรุปที่ว่า wt และ mpg
สัมพันธ์กันทางลบก็ไม่ได้เปลี่ยนแปลงไป
Scatter Plot
การสร้าง scatter plot พร้อม fit line ทำโดยใช้คำสั่งจากแพ็คเกจ ggplot2
- ใช้คำสั่ง
ggplot(data, aes(x, y))เพื่อกำหนดชุดข้อมูลและ aesthetic mapping - บวก
geom_point()สร้าง scatter plot - บวก
geom_smooth(method = , se = )เพื่อสร้างเส้นสมการทำนาย fit line โดยกำหนดตัวเลือกmethod = lmเพื่อสร้างเส้นตรงทำนาย และกำหนดตัวเลือกse = TRUEเพื่อวาด confidence interval รอบเส้นทำนาย fit line (ค่าse = TRUEเป็นค่าตั้งต้น แม้จะไม่ใส่ก็จะแสดงให้โดยอัตโนมัติ)
ggplot(mtcars, aes(x = wt, y = mpg)) +
geom_point() + # scatter dots
geom_smooth(method = lm, se = TRUE) + #add a linear fit line to the previous plot
theme_classic() # optional theme to make a graph look nice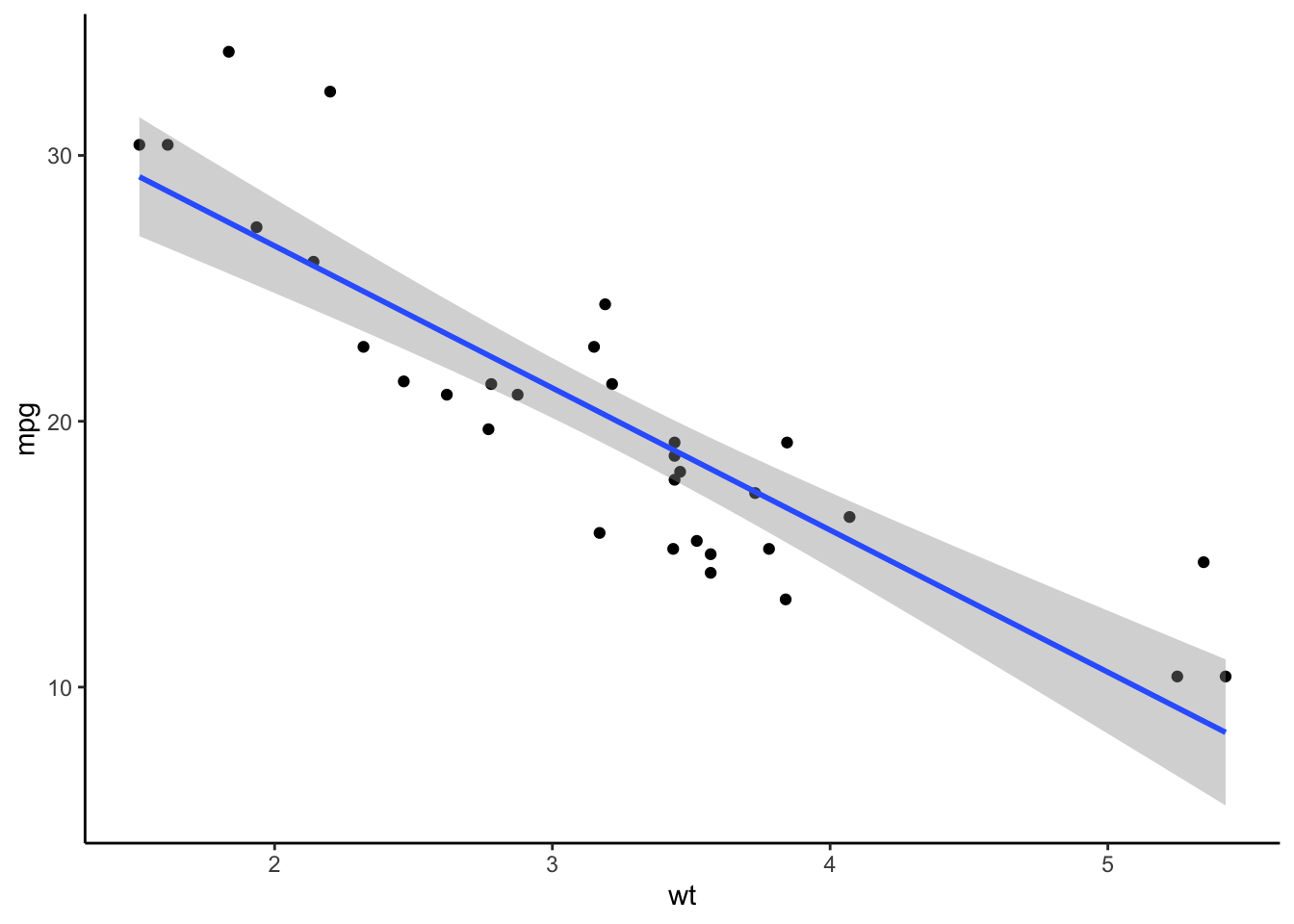
Copyright © 2022 Kris Ariyabuddhiphongs