Lab 11: Mediation Analysis
Kris Ariyabuddhiphongs
Apr 20, 2022
# load all packages for this tutorial
library(psych)
library(lavaan)Mediation Analysis
เราจะใช้ชุดข้อมูล Tal.Or จาก psych
X = cond ตัวแปรเงื่อนไขการทดลอง 0 = low media importance; 1
= high media importance ตัวแปรนี้มีแค่สองระดับและถูกเขียนในรูป dummy code แล้ว
จึงสามารถนำมาใส่สมการ regression ได้ แม้ไม่ได้แปลงเป็น factor
M = pmi presumed media influence
ความรู้สึกว่าตนเองได้รับอิทธิพลจากสื่อเพียงใด
Y = reaction ปฏิกิริยาต่อเรื่องที่อ่านในการทดลอง (เช่น
บทความบอกว่าน้ำตาลจะขาดตลาอด คุณจะไปซื้อน้ำตาลมาตุนไหม)
data(Tal.Or)
media <- Tal.Or
head(media)## cond pmi import reaction gender age
## 1 1 7.0 6 5.25 1 51
## 2 0 6.0 1 1.25 1 40
## 3 1 5.5 6 5.00 1 26
## 4 0 6.5 6 2.75 2 21
## 5 0 6.0 5 2.50 1 27
## 6 0 5.5 1 1.25 1 25Calculation
การวิเคราะห์ตัวแปรส่งผ่านแบบง่าย (มี X, Y, M อย่างละตัว) จะต้องใช้สมการถดถอย 2 สมการ
สมการแรกใช้หาความสัมพันธ์ระหว่างตัวแปรทำนาย X กับตัวแปรส่งผ่าน M
เส้น a: M ~ X (M is regressed on X)
lm(pmi ~ cond, media) # if the model is called directly, a short output is shown. ##
## Call:
## lm(formula = pmi ~ cond, data = media)
##
## Coefficients:
## (Intercept) cond
## 5.3769 0.4765เนื่องจาก cond เป็นตัวแปรจัดประเภท (ทำเป็น dummy) ค่า
coefficient จึงแสดงความแตกต่างระหว่างสองกลุ่ม เห็นได้ว่าเงื่อนไข high media
importance มี pmi สูงกว่า
สมการที่ 2 เป็นการทำนายตัวแปร Y โดยใช้ทั้งตัวแปร X และ M เพื่อหาเส้น b และ c’
เส้น b และ c’ : Y ~ b * M + c * X
lm(reaction ~ pmi + cond, media)##
## Call:
## lm(formula = reaction ~ pmi + cond, data = media)
##
## Coefficients:
## (Intercept) pmi cond
## 0.5269 0.5064 0.2544ค่า coefficient ของ pmi คือ เส้น b
ค่า coefficient ของ cond คือ เส้น c’ หรือ direct effect เป็นความสัมพันธ์ที่ยังเหลืออยู่จาก X ไป Y เมื่อส่งผ่าน M ไปแล้ว
เส้นอิทธิพลทางอ้อม Indirect effect (ab)
เกิดจากการนำค่า coefficient a และ b มาคูณกัน
ab <- 0.4765 * 0.5064
ab## [1] 0.2412996การทดสอบ indirect effect จะใช้วิธี bootstrap ซึ่งจะทำได้ผ่านโปรแกรมต่าง ๆ
PROCESS v4.1 for R
Macro โดย Andrew Hayes https://www.processmacro.org/download.html
วิธีใช้
- Download ไฟล์ และ unzip
- เปิดไฟล์ process.R
- Run All แล้วรอสักพัก
- จะมี Functions ที่ชื่อว่า
processขึ้นมาอยู่ใน environment - ต้อง Run script นี้ใหม่ทุกครั้งหลังจากปิด R
หรือ save process.R ไว้ใน working directory แล้วใช้คำสั่ง
source()
source("process.R")##
## ********************** PROCESS for R Version 4.1 **********************
##
## Written by Andrew F. Hayes, Ph.D. www.afhayes.com
## Documentation available in Hayes (2022). www.guilford.com/p/hayes3
##
## ***********************************************************************
##
## PROCESS is now ready for use.
## Copyright 2022 by Andrew F. Hayes ALL RIGHTS RESERVED
## Workshop schedule at http://haskayne.ucalgary.ca/CCRAM
## ในคำสั่งของ process() เราจะต้องระบุบทบาทของตัวแปรแต่ละตัว
และเลือกรหัส model ที่ Hayes กำหนดไว้ (สามารถหาอ่านได้ในหนังสือของ
Hayes) สำหรับ simple mediation ใช้ model = 4
process(data = media, y = "reaction", x = "cond", m = "pmi", model = 4, boot = 5000, seed = 17889)##
## ********************** PROCESS for R Version 4.1 **********************
##
## Written by Andrew F. Hayes, Ph.D. www.afhayes.com
## Documentation available in Hayes (2022). www.guilford.com/p/hayes3
##
## ***********************************************************************
##
## Model : 4
## Y : reaction
## X : cond
## M : pmi
##
## Sample size: 123
##
## Custom seed: 17889
##
##
## ***********************************************************************
## Outcome Variable: pmi
##
## Model Summary:
## R R-sq MSE F df1 df2 p
## 0.1808 0.0327 1.7026 4.0878 1.0000 121.0000 0.0454
##
## Model:
## coeff se t p LLCI ULCI
## constant 5.3769 0.1618 33.2222 0.0000 5.0565 5.6973
## cond 0.4765 0.2357 2.0218 0.0454 0.0099 0.9431
##
## ***********************************************************************
## Outcome Variable: reaction
##
## Model Summary:
## R R-sq MSE F df1 df2 p
## 0.4538 0.2059 1.9404 15.5571 2.0000 120.0000 0.0000
##
## Model:
## coeff se t p LLCI ULCI
## constant 0.5269 0.5497 0.9585 0.3397 -0.5615 1.6152
## cond 0.2544 0.2558 0.9943 0.3221 -0.2522 0.7609
## pmi 0.5064 0.0970 5.2185 0.0000 0.3143 0.6986
##
## ***********************************************************************
## Bootstrapping progress:
##
|
| | 0%
|
| | 1%
|
|> | 1%
|
|> | 2%
|
|>> | 2%
|
|>> | 3%
|
|>> | 4%
|
|>>> | 4%
|
|>>> | 5%
|
|>>> | 6%
|
|>>>> | 6%
|
|>>>> | 7%
|
|>>>>> | 7%
|
|>>>>> | 8%
|
|>>>>> | 9%
|
|>>>>>> | 9%
|
|>>>>>> | 10%
|
|>>>>>>> | 10%
|
|>>>>>>> | 11%
|
|>>>>>>> | 12%
|
|>>>>>>>> | 12%
|
|>>>>>>>> | 13%
|
|>>>>>>>> | 14%
|
|>>>>>>>>> | 14%
|
|>>>>>>>>> | 15%
|
|>>>>>>>>>> | 15%
|
|>>>>>>>>>> | 16%
|
|>>>>>>>>>> | 17%
|
|>>>>>>>>>>> | 17%
|
|>>>>>>>>>>> | 18%
|
|>>>>>>>>>>> | 19%
|
|>>>>>>>>>>>> | 19%
|
|>>>>>>>>>>>> | 20%
|
|>>>>>>>>>>>>> | 20%
|
|>>>>>>>>>>>>> | 21%
|
|>>>>>>>>>>>>> | 22%
|
|>>>>>>>>>>>>>> | 22%
|
|>>>>>>>>>>>>>> | 23%
|
|>>>>>>>>>>>>>>> | 23%
|
|>>>>>>>>>>>>>>> | 24%
|
|>>>>>>>>>>>>>>> | 25%
|
|>>>>>>>>>>>>>>>> | 25%
|
|>>>>>>>>>>>>>>>> | 26%
|
|>>>>>>>>>>>>>>>> | 27%
|
|>>>>>>>>>>>>>>>>> | 27%
|
|>>>>>>>>>>>>>>>>> | 28%
|
|>>>>>>>>>>>>>>>>>> | 28%
|
|>>>>>>>>>>>>>>>>>> | 29%
|
|>>>>>>>>>>>>>>>>>> | 30%
|
|>>>>>>>>>>>>>>>>>>> | 30%
|
|>>>>>>>>>>>>>>>>>>> | 31%
|
|>>>>>>>>>>>>>>>>>>>> | 31%
|
|>>>>>>>>>>>>>>>>>>>> | 32%
|
|>>>>>>>>>>>>>>>>>>>> | 33%
|
|>>>>>>>>>>>>>>>>>>>>> | 33%
|
|>>>>>>>>>>>>>>>>>>>>> | 34%
|
|>>>>>>>>>>>>>>>>>>>>> | 35%
|
|>>>>>>>>>>>>>>>>>>>>>> | 35%
|
|>>>>>>>>>>>>>>>>>>>>>> | 36%
|
|>>>>>>>>>>>>>>>>>>>>>>> | 36%
|
|>>>>>>>>>>>>>>>>>>>>>>> | 37%
|
|>>>>>>>>>>>>>>>>>>>>>>> | 38%
|
|>>>>>>>>>>>>>>>>>>>>>>>> | 38%
|
|>>>>>>>>>>>>>>>>>>>>>>>> | 39%
|
|>>>>>>>>>>>>>>>>>>>>>>>> | 40%
|
|>>>>>>>>>>>>>>>>>>>>>>>>> | 40%
|
|>>>>>>>>>>>>>>>>>>>>>>>>> | 41%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>> | 41%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>> | 42%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>> | 43%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>> | 43%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>> | 44%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 44%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 45%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 46%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 46%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 47%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 48%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 48%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 49%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 49%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 50%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 51%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 51%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 52%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 52%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 53%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 54%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 54%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 55%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 56%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 56%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 57%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 57%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 58%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 59%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 59%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 60%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 60%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 61%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 62%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 62%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 63%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 64%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 64%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 65%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 65%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 66%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 67%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 67%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 68%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 69%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 69%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 70%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 70%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 71%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 72%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 72%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 73%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 73%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 74%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 75%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 75%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 76%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 77%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 77%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 78%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 78%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 79%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 80%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 80%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 81%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 81%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 82%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 83%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 83%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 84%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 85%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 85%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 86%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 86%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 87%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 88%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 88%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 89%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 90%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 90%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 91%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 91%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 92%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 93%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 93%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 94%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 94%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 95%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 96%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 96%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 97%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 98%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 98%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> | 99%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>| 99%
|
|>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>| 100%
##
## **************** DIRECT AND INDIRECT EFFECTS OF X ON Y ****************
##
## Direct effect of X on Y:
## effect se t p LLCI ULCI
## 0.2544 0.2558 0.9943 0.3221 -0.2522 0.7609
##
## Indirect effect(s) of X on Y:
## Effect BootSE BootLLCI BootULCI
## pmi 0.2413 0.1300 0.0050 0.5139
##
## ******************** ANALYSIS NOTES AND ERRORS ************************
##
## Level of confidence for all confidence intervals in output: 95
##
## Number of bootstraps for percentile bootstrap confidence intervals: 5000psych package
มีคำสั่งชื่อ mediate()
set.seed(17889) #set seed to the same number for consistent results
m <- mediate(y = "reaction", x = "cond", m = "pmi", data = media, n.iter = 5000)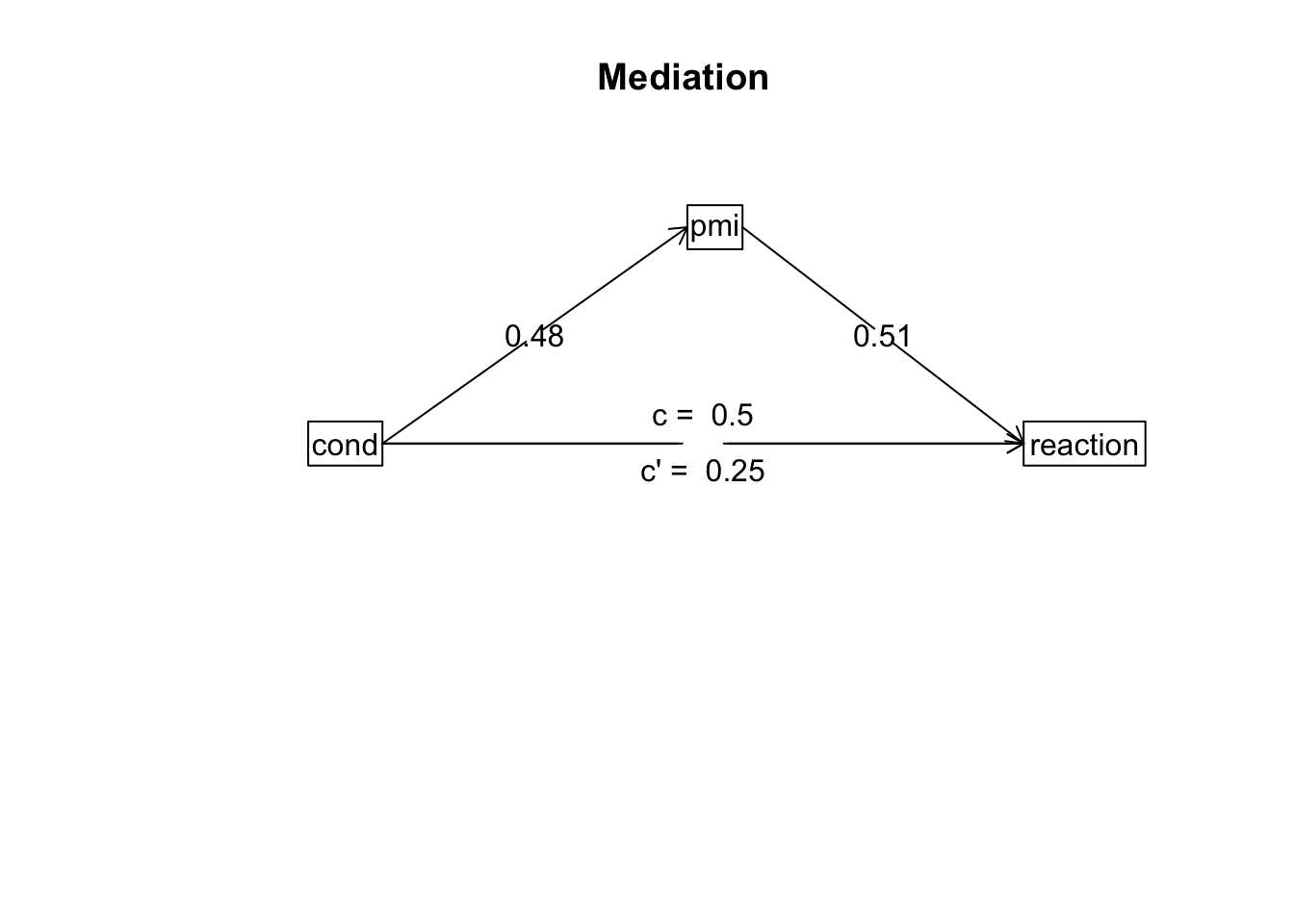
summary(m)## Call: mediate(y = "reaction", x = "cond", m = "pmi", data = media,
## n.iter = 5000)
##
## Direct effect estimates (traditional regression) (c') X + M on Y
## reaction se t df Prob
## Intercept 0.53 0.55 0.96 120 3.40e-01
## cond 0.25 0.26 0.99 120 3.22e-01
## pmi 0.51 0.10 5.22 120 7.66e-07
##
## R = 0.45 R2 = 0.21 F = 15.56 on 2 and 120 DF p-value: 9.83e-07
##
## Total effect estimates (c) (X on Y)
## reaction se t df Prob
## Intercept 3.25 0.19 17.05 121 5.68e-34
## cond 0.50 0.28 1.79 121 7.66e-02
##
## 'a' effect estimates (X on M)
## pmi se t df Prob
## Intercept 5.38 0.16 33.22 121 1.16e-62
## cond 0.48 0.24 2.02 121 4.54e-02
##
## 'b' effect estimates (M on Y controlling for X)
## reaction se t df Prob
## pmi 0.51 0.1 5.22 120 7.66e-07
##
## 'ab' effect estimates (through all mediators)
## reaction boot sd lower upper
## cond 0.24 0.24 0.13 0 0.52lavaan package
แพ็คเกจนี้ใช้วิเคราะห์โมเดลสมการเชิงโครงสร้าง (Structural Equation Model; SEM)
เราจะต้องเขียนโมเดลและกำหนดชื่อพารามิเตอร์ที่ต้องการจะทดสอบ จากนั้น fit model
ด้วยคำสั่ง sem() และเลือกวิธีคำนวณ Standard Error ด้วย
"bootstrap" และกำหนดจำนวนครั้งที่จะ
bootstrap = 5000
ผลที่ได้จากคำสั่งนี้จะแตกต่างจาก packages ก่อนหน้าเล็กน้อย เนื่องจากมันจะคำนวณการทดสอบนัยสำคัญของพารามิเตอร์ทุกตัว (ทั้ง a, b, c, และ ab) ด้วยวิธี bootstrap ทั้งหมด ในขณะที่ package ก่อนหน้าจะใช้วิธี bootstrap เฉพาะ ab
set.seed(17889)
model = " # Regression models
pmi ~ a * cond
reaction ~ c * cond + b * pmi
# direct effect
direct := c
# indirect effect (a*b)
indirect := a*b
# total effect
total := c + (a*b)"
media.fit <- sem(model, data = media, se = "bootstrap", bootstrap = 5000)
summary(media.fit, ci = TRUE, rsquare = TRUE)## lavaan 0.6-12 ended normally after 1 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 123
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Bootstrap
## Number of requested bootstrap draws 5000
## Number of successful bootstrap draws 5000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
## pmi ~
## cond (a) 0.477 0.235 2.028 0.043 0.003 0.940
## reaction ~
## cond (c) 0.254 0.258 0.984 0.325 -0.264 0.733
## pmi (b) 0.506 0.080 6.344 0.000 0.341 0.655
##
## Variances:
## Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
## .pmi 1.675 0.284 5.895 0.000 1.120 2.247
## .reaction 1.893 0.190 9.981 0.000 1.483 2.231
##
## R-Square:
## Estimate
## pmi 0.033
## reaction 0.206
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
## direct 0.254 0.258 0.984 0.325 -0.264 0.733
## indirect 0.241 0.131 1.844 0.065 0.002 0.517
## total 0.496 0.274 1.807 0.071 -0.036 1.025parameterEstimates(media.fit, se = TRUE, boot.ci.type = "perc") #show summary of parameter estimates for easy readout## lhs op rhs label est se z pvalue ci.lower ci.upper
## 1 pmi ~ cond a 0.477 0.235 2.028 0.043 0.003 0.940
## 2 reaction ~ cond c 0.254 0.258 0.984 0.325 -0.264 0.733
## 3 reaction ~ pmi b 0.506 0.080 6.344 0.000 0.341 0.655
## 4 pmi ~~ pmi 1.675 0.284 5.895 0.000 1.120 2.247
## 5 reaction ~~ reaction 1.893 0.190 9.981 0.000 1.483 2.231
## 6 cond ~~ cond 0.249 0.000 NA NA 0.249 0.249
## 7 direct := c direct 0.254 0.258 0.984 0.325 -0.264 0.733
## 8 indirect := a*b indirect 0.241 0.131 1.844 0.065 0.002 0.517
## 9 total := c+(a*b) total 0.496 0.274 1.807 0.071 -0.036 1.025จะสังเกตได้ว่าค่า 95% bootstrap CI จาก lavaan จะแตกต่างไปจาก process หรือ psych ตรงนี้อาจะเป็นเพราะโค้ดมีวิธีการใช้ตัวเลขสุ่มแตกต่างกันเล็กน้อย แต่ไม่ส่งผลต่อความน่าเชื่อถือของผล เพื่อให้สามารถวิเคราะห์ผลซ้ำได้ เราจึงควรระบุชื่อโปรแกรม เวอร์ชัน และ seed ที่ใช้ในการวิเคราะห์ด้วย
Copyright © 2022 Kris Ariyabuddhiphongs