Lab 09: Multiple Regression

โหลดแพ็คเกจที่จะต้องใช้ในแบบฝึกหัดนี้

library(psych)
library(car)
library(carData)

1. Multiple Regression

Linear model

การวิเคราะห์ถดถอยพหุคูณนี้จะใช้ชุดข้อมูล Prestige จากแพ็คเกจ carData ข้อมูลชุดนี้มีอาชีพเป็น observation (แต่ละแถวแทนอาชีพหนึ่งอาชีพ เคสเป็นระดับอาชีพ ไม่ใช่ระดับบุคคล) มีตัวแปรต่าง ๆ ดังนี้

education = ระยะเวลาการศึกษาเฉลี่ยของผู้ประกอบอาชีพนั้น

income = รายได้เฉลี่ยของผู้ประกอบอาชีพ หน่วยเป็นดอลลาห์

women = ร้อยละของผู้หญิงในอาชีพ

prestige = คะแนนมาตรความมีเกียรติ (Pineo-Porter prestige score) ของอาชีพ

census = รหัสอาชีพในสำมะโนประชากรของแคนาดา

type = ประเภทของอาชีพ bc = Blue Collar; prof = Professional, Managerial, and Technical; wc = White Collar

เราจะใช้คำสั่ง lm() เพื่อสร้างโมเดลเชิงเส้นตรงทำนายความีเกียรติของอาชีพ prestige ด้วย education, income, และ women

# Import data 
dat <- carData::Prestige
str(dat)

## 'data.frame':    102 obs. of  6 variables:
##  $ education: num  13.1 12.3 12.8 11.4 14.6 ...
##  $ income   : int  12351 25879 9271 8865 8403 11030 8258 14163 11377 11023 ...
##  $ women    : num  11.16 4.02 15.7 9.11 11.68 ...
##  $ prestige : num  68.8 69.1 63.4 56.8 73.5 77.6 72.6 78.1 73.1 68.8 ...
##  $ census   : int  1113 1130 1171 1175 2111 2113 2133 2141 2143 2153 ...
##  $ type     : Factor w/ 3 levels "bc","prof","wc": 2 2 2 2 2 2 2 2 2 2 ...

prestige.lm <- lm(prestige ~ education + income + women, data = dat)
summary(prestige.lm)

## 
## Call:
## lm(formula = prestige ~ education + income + women, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -19.8246  -5.3332  -0.1364   5.1587  17.5045 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -6.7943342  3.2390886  -2.098   0.0385 *  
## education    4.1866373  0.3887013  10.771  < 2e-16 ***
## income       0.0013136  0.0002778   4.729 7.58e-06 ***
## women       -0.0089052  0.0304071  -0.293   0.7702    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.846 on 98 degrees of freedom
## Multiple R-squared:  0.7982, Adjusted R-squared:  0.792 
## F-statistic: 129.2 on 3 and 98 DF,  p-value: < 2.2e-16

ค่า F ที่มีนัยสำคัญทางสถิติแสดงให้เห็นว่า ตัวแปร X ทั้ง 3 ตัว ร่วมกันทำนายตัวแปร Y ได้อย่างมีนัยสำคัญทางสถิติ (\(R^2 > 0\))

การวิเคราะห์นี้มี intercept 1 ตัว (\(b_0\)) และสัมประสิทธิ์ถดถอย 3 ตัว ได้แก่ \(b_{education}\), \(b_{income}\), \(b_{women}\) ดังนั้น \(df = N - k -1 = 102 - 3 -1 = 98\)

ในการวิเคราะห์นี้พบตัวแปรทำนายที่สัมพันธ์กับ Y อย่างมีนัยสำคัญทางสถิติ คือ education และ income ในขณะที่ women ไม่พบความสัมพันธ์อย่างมีนัยสำคัญ

ค่าสัมประสิทธิ์แต่ละตัวถูกทดสอบว่าแตกต่างจาก 0 หรือไม่ \(H_0: b ≠ 0\) โดยนำค่า b (Estimate) ไปหารด้วยความคลาดเคลื่อน Std. Error จะได้ค่า t value และค่า p-value Pr(>|t|)

Standardized Coefficients

ค่าสัมประสิทธิ์เหล่านี้เป็นอยู่ในหน่วยของคะแนนดิบ หากต้องการเปรียบเทียบนำ้หนักของแต่ละตัวแปรในโมเดลนี้ ต้องใช้ค่าสัมประสิทธิ์มาตรฐาน (standardized coefficients)

ค่า standardized coefficients จริง ๆ แล้วก็คือ การนำค่าตัวแปรทุกตัวไปแปลงเป็น standard score (z-scores) ก่อนแล้วนำมาใส่ในโมเดล ดังนั้นเราสามารถคำนวณค่า standardized coefficient เองได้ด้วย

prestige.zlm <- lm(scale(prestige) ~ scale(education) + scale(income) + scale(women), data = dat)
summary(prestige.zlm)

## 
## Call:
## lm(formula = scale(prestige) ~ scale(education) + scale(income) + 
##     scale(women), data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.15229 -0.30999 -0.00793  0.29984  1.01744 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      -2.258e-16  4.516e-02   0.000     1.00    
## scale(education)  6.640e-01  6.164e-02  10.771  < 2e-16 ***
## scale(income)     3.242e-01  6.855e-02   4.729 7.58e-06 ***
## scale(women)     -1.642e-02  5.607e-02  -0.293     0.77    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4561 on 98 degrees of freedom
## Multiple R-squared:  0.7982, Adjusted R-squared:  0.792 
## F-statistic: 129.2 on 3 and 98 DF,  p-value: < 2.2e-16

Residual plots

หากเรา plot(model) โปรแกรม R จะแสดงกราฟที่ใช้เพื่อวินิจฉัยโมเดลมาให้

กราฟ Residuals vs Fitted ใช้ตรวจสอบ linearity assumption กราฟจะแสดงค่า \(\hat{Y}\) (Fitted) และ \(e\) (Residuals) หากความสัมพันธ์ระหว่างผลรวมเชิงเส้นตรงของตัวแปร X สัมพันธ์ทางบวกกับ Y เส้นสีแดงจะเป็นเส้นตรงตามเส้นประ

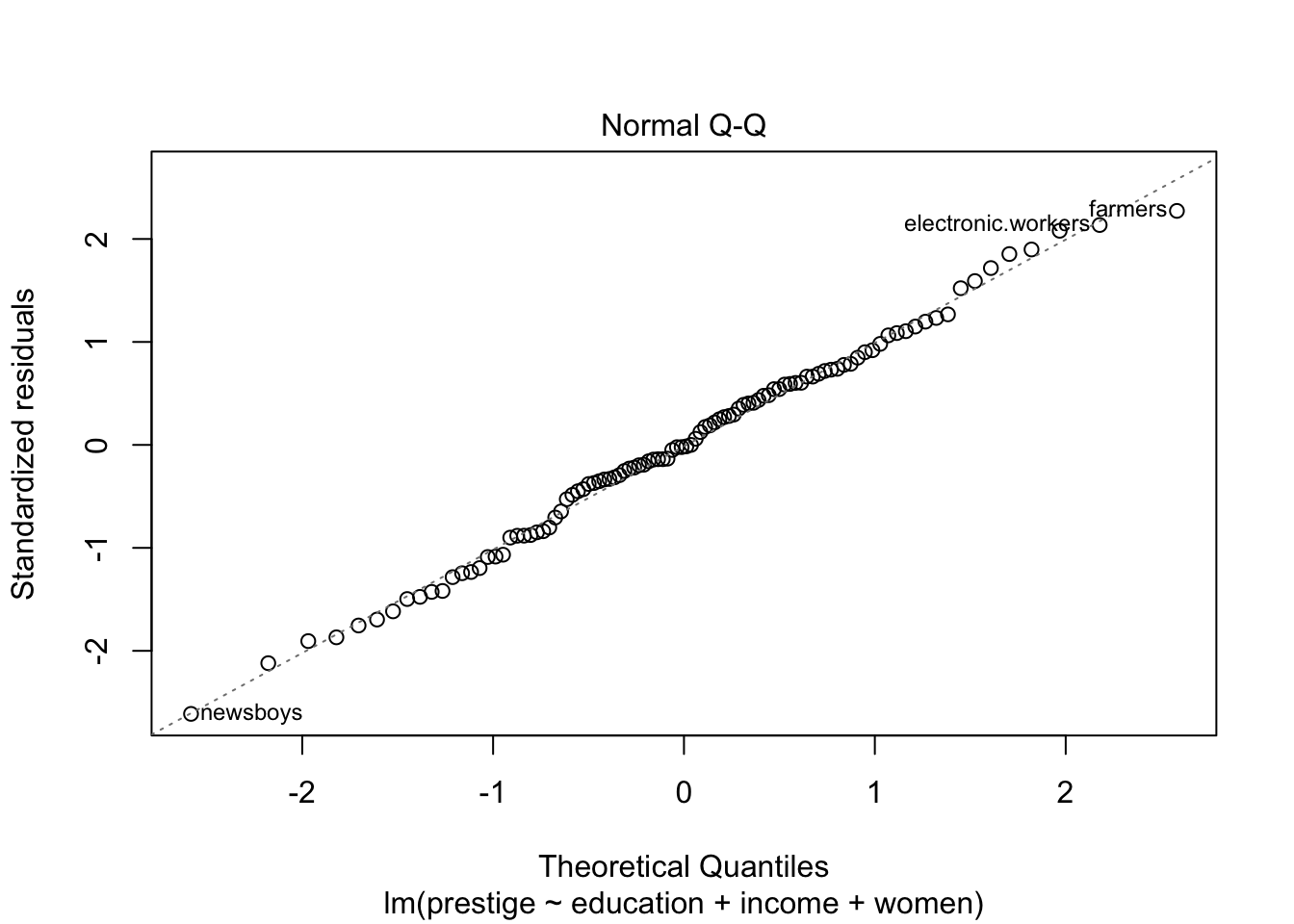
กราฟ Normal Q-Q ใช้ดู normality ของ residuals หากความคลาดเคลื่อนมีการกระจายตัวเป็นปกติ จุดคะแนนต่าง ๆ จะเรียงตัวอยู่บนเส้นแทยง

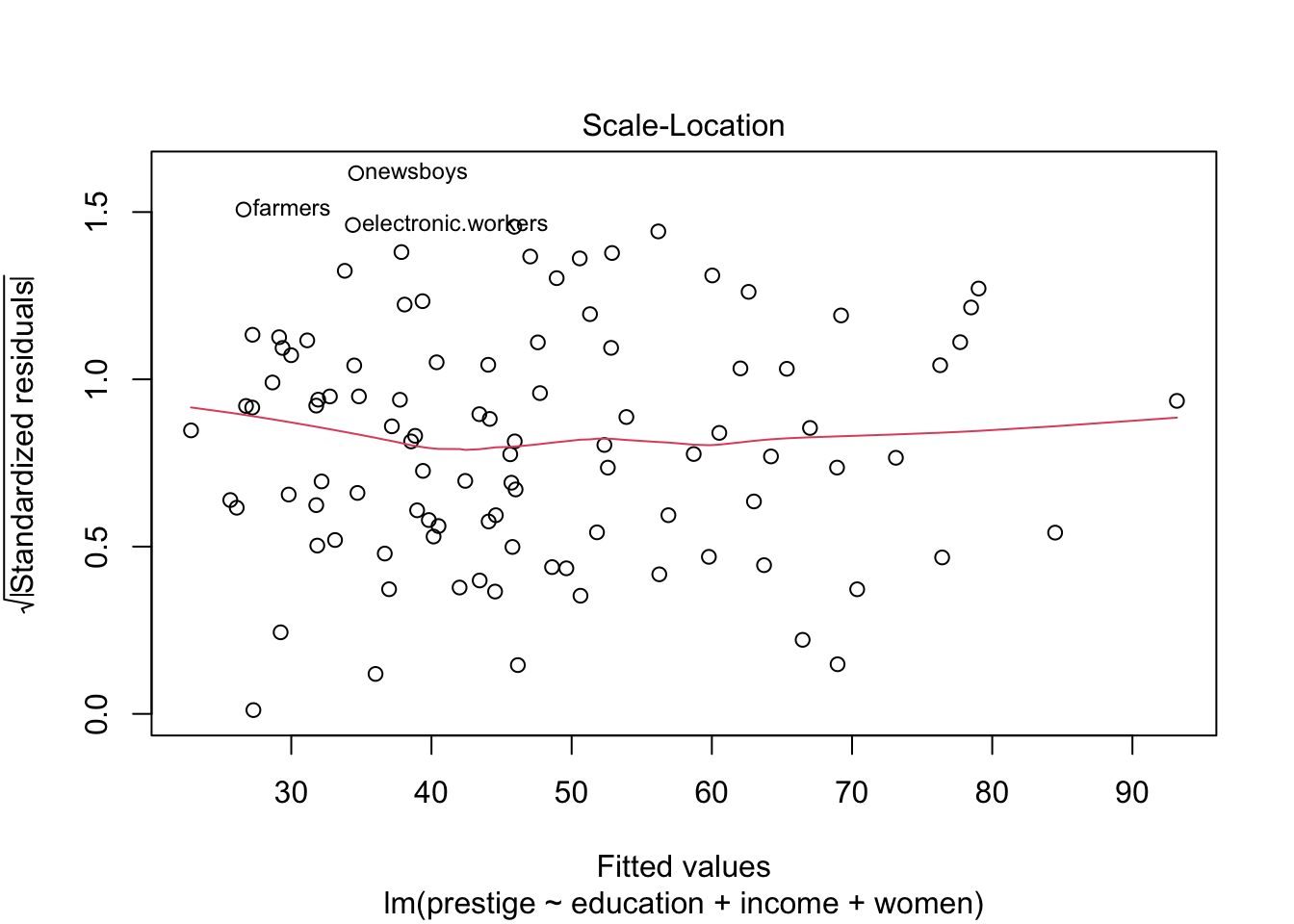
กราฟ Scale-Location หรือ Spread-Location ใช้ตรวจสอบ homoscedasticity (homogeneity of variance สำหรับ regression) ความแปรปรวนของ residual ควรเท่ากันในทุกช่วงคะแนน \(\hat{Y}\) ดังนั้นการกระจายของจุดต่าง ๆ จะกว้างพอ ๆ กันตลอดแกน X ทำให้ได้เส้นสีแดงที่เป็นเส้นตรงแนวนอน

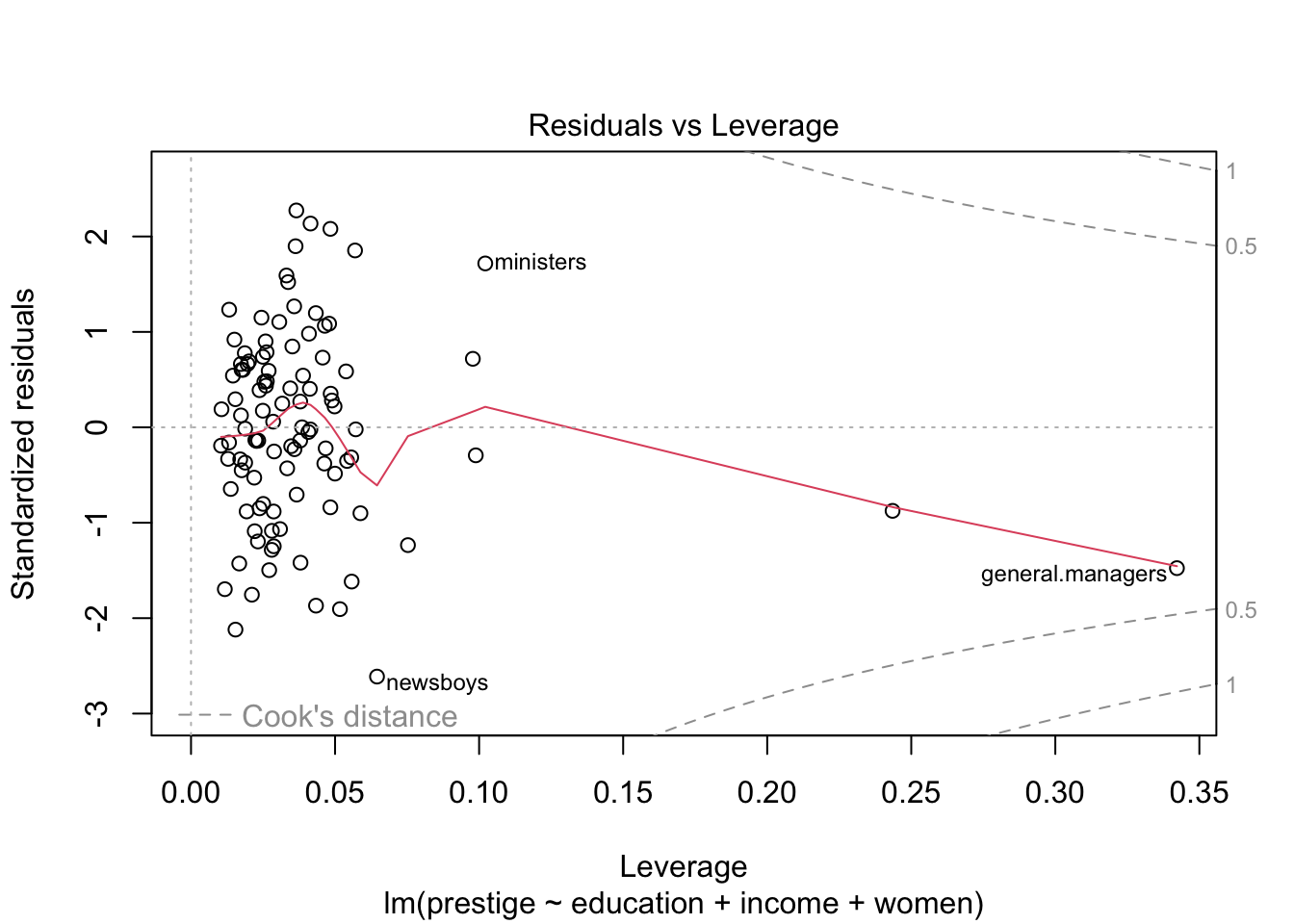
กราฟ Residuals vs Leverage แสดงถึงข้อมูลสุดโต่งหรือข้อมูลที่มีอิทธิพลต่อโมเดลอย่างมาก ข้อมูลที่มีอิทธิพลสูงนี้สามารถทำให้ความชันของสมการเปลี่ยนแปลงไปได้ หากมีหรือไม่มีข้อมูลจุดนั้นอยู่ กรณีที่สุดโต่งจะมีค่า Leverage สูงแยกออกมาจากข้อมูลส่วนใหญ่

plot(prestige.lm)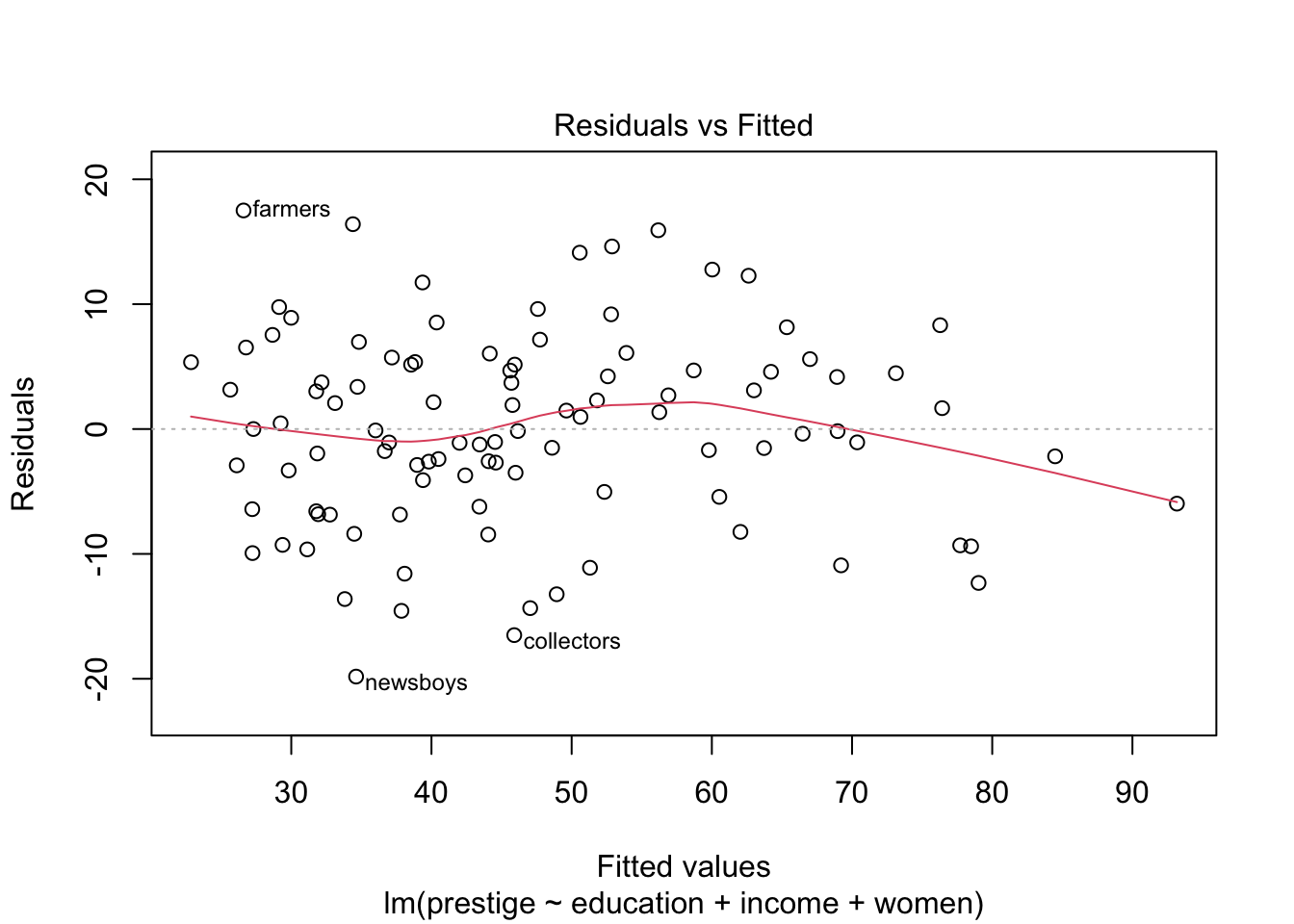

คำสั่ง plot() นี้ทำให้เราเห็น assumption ต่าง ๆ ของโมเดลในภาพรวม แต่ยังไม่ช่วยบอกว่าตัวแปร X ตัวใดที่อาจจะเป็นต้นเหตุของปัญหา

เราสามารถใช้คำสั่ง residualPlots() ในแพ็คเกจ car เพื่อตรวจสอบ linearity assumption เป็นรายตัวแปร X ได้ นอกจากนี้คำสั่งจะให้ค่าทดสอบของ Tukey’s nonadditivity test มาด้วย หากมีนัยสำคัญทางสถิติแสดงว่าความสัมพันธ์ของตัวแปร X นั้นกับ Y ไม่เป็นเส้นตรง

ลองพิจารณาค่าสถิติและกราฟดูว่าตัวแปรใดน่าจะต้นเหตุของ nonlinearity ในโมเดลนี้

residualPlots(prestige.lm)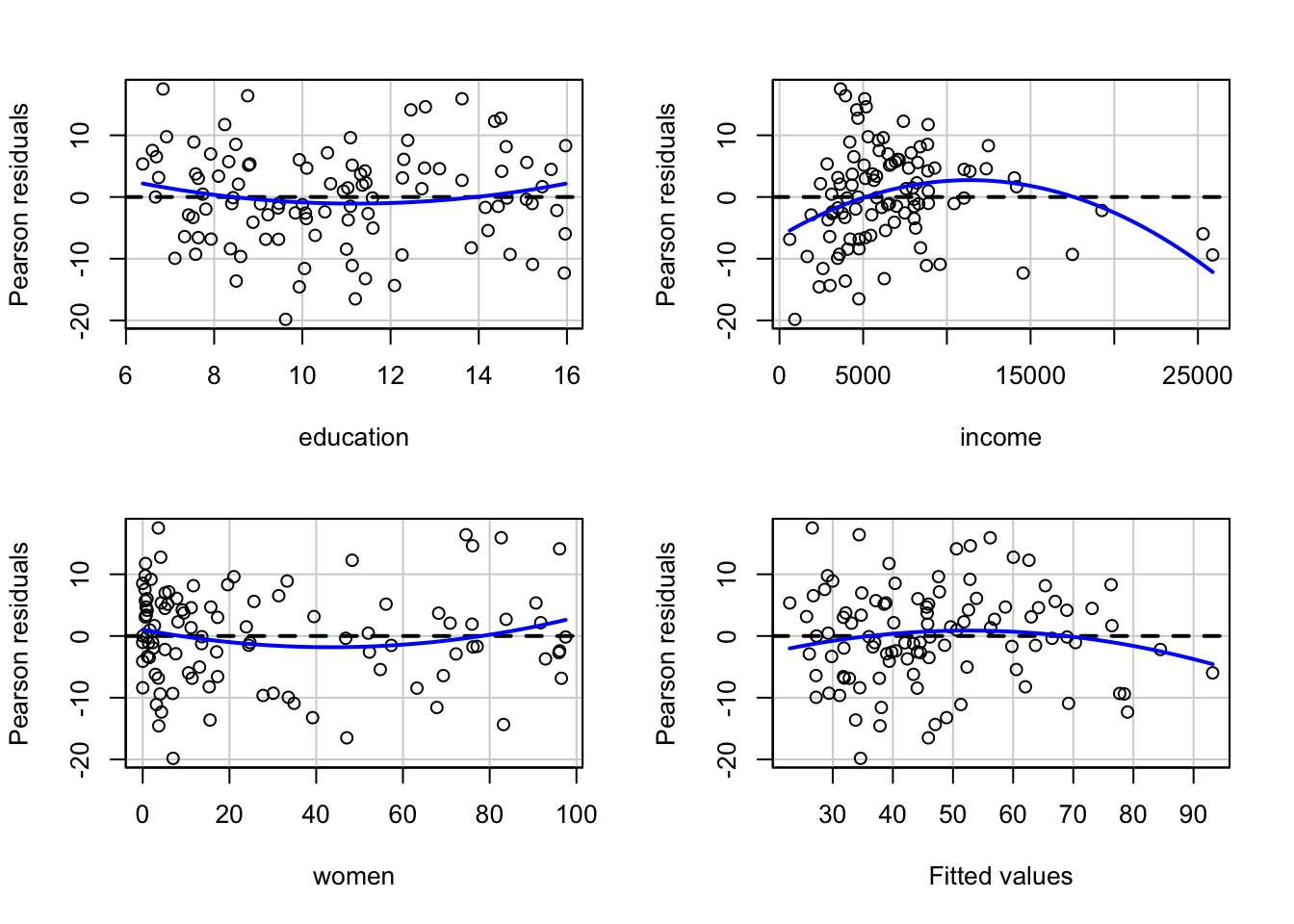

##            Test stat Pr(>|Test stat|)    
## education     1.3268           0.1877    
## income       -4.2815        4.366e-05 ***
## women         1.4427           0.1523    
## Tukey test   -1.4169           0.1565    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

อย่างไรก็ดี การใช้ตาตรวจดูค่าความผิดปกติต่าง ๆ อาจมีอคติหรือข้อผิดพลาด ทำให้ตัดสินใจผิดพลาดได้ว่าข้อมูลที่เป็นปัญหา คือ จุดใด ดังนั้นวิธีการตรวจทางสายตาจึงควรใช้ควบคู่กับการทดสอบด้วย

2. Detecting Extreme Cases

2.1 Leverage

เลฟเวอเรจ (leverage) คือ กรณีที่ค่าของตัวแปรทำนาย \(X_i\) นั้นมีระยะห่างจากค่าเฉลี่ย \(\bar{X}\) อย่างมาก (ไม่เกี่ยวกับค่า Y) ในแบบฝึกหัดที่ผ่าน ๆ มา เราได้ใช้วิธีแปลงคะแนนค่า X เป็นคะแนนมาตรฐาน (z score) เพื่อดูว่าค่านั้นสุดโต่งหรือไม่ นี่คือแนวคิดของการหา univariate outlier คือพิจารณาค่าสุดโต่งของตัวแปรเดียว (ไม่พิจารณาร่วมกับตัวแปรอื่น) หากเรานำค่า z ที่ได้ไปยกกำลังสอง เราจะได้สูตรดังนี้

\[ Z^2_{X_i} = \bigg{(}\frac{X_i - \bar{X}}{s_{X}^2}\bigg{)}^2 \]

เนื่องจากค่า \(Z^2\) เป็นค่าทางบวกเสมอที่แสดงถึงความห่างของค่าคะแนน \(X_i\) จากค่าเฉลี่ย \(\bar{X}\) โดยปกติแล้วเราจะใช้เกณฑ์ที่ ±3 SD เป็นจุดตัดของค่าสุดโต่ง

Mahalanobis distance

แต่ในกรณีของการถดถอยพหุคูณ (multiple regression; MR) ค่าตัวแปร X ที่สุดโต่งอาจต้องพิจารณาร่วมกับตัวแปร X อื่น ๆ ด้วย เช่น คนที่สูง 180 อาจจะไม่นับว่าเป็นค่าสุดโต่งในชุดข้อมูล แต่ผู้หญิงที่สูง 180 เป็นค่าที่มีเลฟเวอเรจสูง (พิจารณาตัวแปรเพศและความสูงร่วมกันแล้วมีโอกาสเกิดขึ้นน้อย) เนื่องจากต้องพิจารณาหลายตัวแปรร่วมกันจึงเรียกว่าเป็น multivariate outlier โดยค่าสถิติที่ใช้พิจารณาก็พัฒนาต่อเนื่องมาจากสูตรด้านบนโดยใช้พีชคณิตเมทริกซ์ ได้เป็นค่าที่เรียกว่า Mahalanobis distance

เราจะใช้คำสั่ง outlier(x, plot = TRUE, bad = 5, na.rm = TRUE) ในแพ็คเกจ psych

x คือ ชุดตัวแปร X

plot คือต้องการให้สร้างกราฟ QQ หรือไม่ (ค่าตั้งต้น = TRUE)

bad คือ ให้แสดงเคสที่มีปัญหาบนกราฟ (ค่าตั้งต้น = 5 ตัวที่มีปัญหามากที่สุด)

na.rm คือ ให้ลบข้อมูลที่มี missing ทิ้ง (ค่าตั้งต้น = TRUE)

predictors <- dat[c("education", "income", "women")]
dat$maha_dis <- psych::outlier(predictors)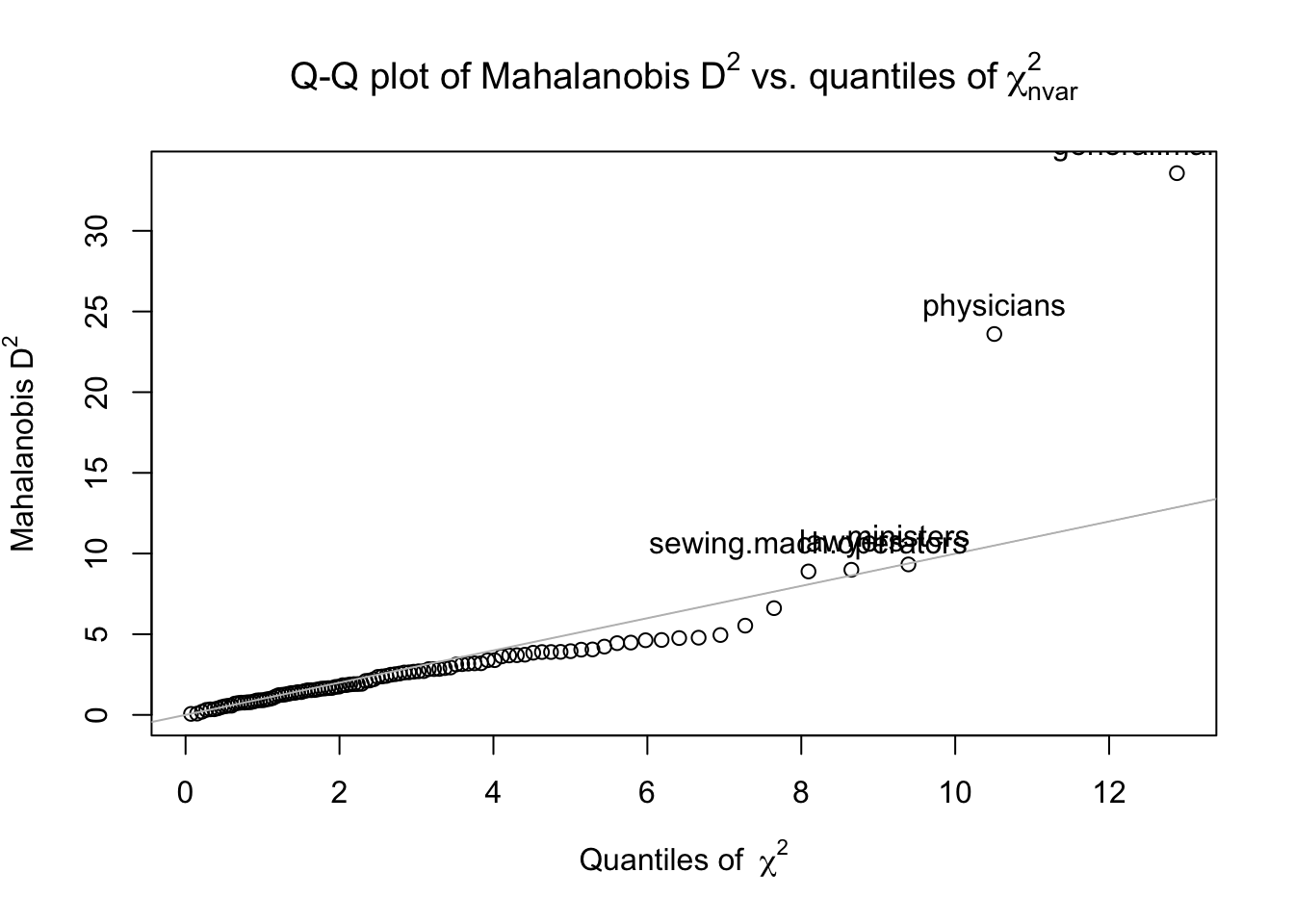

head(dat)

##                     education income women prestige census type   maha_dis
## gov.administrators      13.11  12351 11.16     68.8   1113 prof  1.7323152
## general.managers        12.26  25879  4.02     69.1   1130 prof 33.5731939
## accountants             12.77   9271 15.70     63.4   1171 prof  0.7825381
## purchasing.officers     11.42   8865  9.11     56.8   1175 prof  0.4787457
## chemists                14.62   8403 11.68     73.5   2111 prof  3.6997050
## physicists              15.64  11030  5.13     77.6   2113 prof  4.4454380

#calculate p value for Mahalanobis distance with Chi-square test with df = k- 1, where k = number of variables.
dat$maha_p <- pchisq(dat$maha_dis, df = 2, lower.tail = FALSE) # We only look for large MD. Therefore, only upper tail of distribution. 
head(dat)

##                     education income women prestige census type   maha_dis       maha_p
## gov.administrators      13.11  12351 11.16     68.8   1113 prof  1.7323152 4.205644e-01
## general.managers        12.26  25879  4.02     69.1   1130 prof 33.5731939 5.124761e-08
## accountants             12.77   9271 15.70     63.4   1171 prof  0.7825381 6.761982e-01
## purchasing.officers     11.42   8865  9.11     56.8   1175 prof  0.4787457 7.871214e-01
## chemists                14.62   8403 11.68     73.5   2111 prof  3.6997050 1.572604e-01
## physicists              15.64  11030  5.13     77.6   2113 prof  4.4454380 1.083142e-01

dat[dat$maha_p < .001, ] # cases with p < .001 are considered outliers.

##                  education income women prestige census type maha_dis       maha_p
## general.managers     12.26  25879  4.02     69.1   1130 prof 33.57319 5.124761e-08
## physicians           15.96  25308 10.56     87.2   3111 prof 23.60481 7.486533e-06

hat values (h-values)

อย่างไรก็ดีค่าสถิติอีกตัวหนึ่งที่ทำหน้าที่เหมือนกับ Mahalanobis distance จะเป็นที่นิยมมากกว่า นั่นคือค่า h values หรือ hat values

ค่า h values จะอยู่ระหว่าง 0 ถึง 1 ทำให้อ่านค่าและกำหนดเกณฑ์ได้ง่ายกว่ามาก โดยมักจะกำหนดให้ค่า hat ต้องไม่เกิน \(2p/n\) โดย p คือ จำนวน parameters ของโมเดล (จำนวน coefficients) และ n คือ จำนวนกลุ่มตัวอย่าง

dat$hat <- hatvalues(prestige.lm)
head(dat)

##                     education income women prestige census type   maha_dis       maha_p        hat
## gov.administrators      13.11  12351 11.16     68.8   1113 prof  1.7323152 4.205644e-01 0.02695556
## general.managers        12.26  25879  4.02     69.1   1130 prof 33.5731939 5.124761e-08 0.34221178
## accountants             12.77   9271 15.70     63.4   1171 prof  0.7825381 6.761982e-01 0.01755182
## purchasing.officers     11.42   8865  9.11     56.8   1175 prof  0.4787457 7.871214e-01 0.01454398
## chemists                14.62   8403 11.68     73.5   2111 prof  3.6997050 1.572604e-01 0.04643466
## physicists              15.64  11030  5.13     77.6   2113 prof  4.4454380 1.083142e-01 0.05381816

p = 3
hat_cutoff <- 2*p/nrow(dat)
high_leverage_cases <- subset(dat, subset = hat > hat_cutoff)
high_leverage_cases

##                          education income women prestige census type  maha_dis       maha_p        hat
## general.managers             12.26  25879  4.02     69.1   1130 prof 33.573194 5.124761e-08 0.34221178
## lawyers                      15.77  19263  5.13     82.3   2343 prof  8.992782 1.114916e-02 0.09884136
## ministers                    14.50   4686  4.14     72.8   2511 prof  9.325301 9.441403e-03 0.10213364
## physicians                   15.96  25308 10.56     87.2   3111 prof 23.604809 7.486533e-06 0.24351491
## osteopaths.chiropractors     14.71  17498  6.91     68.4   3117 prof  6.614742 3.661230e-02 0.07529642
## newsboys                      9.62    918  7.00     14.8   5143 <NA>  5.530371 6.296442e-02 0.06456007
## sewing.mach.operators         6.38   2847 90.67     28.2   8563   bc  8.889789 1.173835e-02 0.09782163

แม้เราจะพบว่ามีกรณีที่ข้อมูลมี leverage สูง แต่ก็ไม่ได้หมายความว่า ค่าเหล่านั้นจะส่งผลต่อโมเดลเสมอไป การตรวจ leverage นี้อาจใช้เพื่อตรวจสอบความถูกต้องของข้อมูลในเบื้องต้น เพื่อดูว่ามีกรณีที่ผิดปกติหรือมีการกรอกข้อมูลผิดหรือไม่ หากข้อมูลไม่ได้มีความผิดปกติอะไร เราอาจเก็บข้อมูลนั้นไว้ก่อนเพื่อไปตรวจสอบ influence ในภายหลัง

2.2 Distance

Distance คือ ระยะห่างของค่า Y แต่ละตัวจากค่า \(\hat{Y}\) (ค่า Y ทำนาย; predicted Y) นั่นก็คือค่าที่ทำให้เกิดความคลาดเคลื่อนในการทำนายสูง (residual)

เคสที่มี distance สูงจะทำให้ความคลาดเคลื่อนของโมเดลสูงไปด้วย และทำให้โมเดลไม่ fit กับข้อมูล (เช่น \(R^2\) น้อยกว่าที่ควรจะเป็น)

Studentized residual

วิธีตรวจสอบว่า residual นั้นมีขนาดใหญ่จนผิดปกติหรือไม่ ทำโดยการแปลง residual เป็น t-score แล้วเปรียบเทียบกับ t-distribution ค่านี้มีชื่อเรียกว่า Studentized residual (มาจากชื่อ Student’s t distribution) ซึ่งเหมาะสำหรับกลุ่มตัวอย่างที่ไม่ใหญ่มาก หากกลุ่มตัวอย่างใหญ่มากจะใช้วิธีแปลงเป็น z-score เทียบกับ normal distribution และเรียกว่า standardized residual

เมื่อแปลงเป็นค่าคะแนน t แล้ว หากทดสอบพบว่าระดับนัยสำคัญ ก็แสดงว่าเป็น outlier

แพ็คเกจ car มีคำสั่งที่ชื่อว่า outlierTest()

outlierTest(prestige.lm)

## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
##           rstudent unadjusted p-value Bonferroni p
## newsboys -2.694442          0.0083101      0.84763

ในโมเดลนี้ newsboys เป็นอาชีพที่มี Studentized residual สูงที่สุด แต่ไม่ถึงระดับนัยสำคัญโดยดูจาก Bonferroni p จึงยังไม่ถือว่าเป็นข้อมูลสุดโต่งในตัวแปร Y

2.3 Influence

Influence คือ อิทธิพลที่เคสนั้นมีต่อสมการถดถอย นั่นคือ ถ้าเคสนี้หายไปค่า b จะเปลี่ยนไปเท่าใด

ค่าที่มี leverage หรือ distance สูงอาจจะไม่ได้ส่งผลต่อโมเดลการถดถอยพหุคูณเสมอไป ค่าเหล่านี้จะทำให้ผลการวิเคราะห์ผิดเพี้ยนไปได้ก็เมื่อค่าเหล่านั้นมีอิทธิพล (influence) ต่อสัมประสิทธิ์ถดถอย นั่นคือ ข้อมูลกรณีนี้ทำให้เกิดการเปลี่ยนแปลงของเส้น fitted line อย่างมาก

Cook’s distance

ค่า Cook’s distance ใช้บอกระดับอิทธิพลของเคสต่อผลการวิเคราะห์ถดถอย (ชื่ออาจทำให้สับสน เพราะเรียกว่า distance แต่ใช้วัด influence) โดยปกติแล้วค่า Cook’s d ที่มากกว่า 0.5 หรือ 1.0 จะถือว่าเป็นกรณีที่ต้องพิจารณาอย่างระมัดระวัง

dat$cook <- cooks.distance(prestige.lm)
head(dat)

##                     education income women prestige census type   maha_dis       maha_p        hat
## gov.administrators      13.11  12351 11.16     68.8   1113 prof  1.7323152 4.205644e-01 0.02695556
## general.managers        12.26  25879  4.02     69.1   1130 prof 33.5731939 5.124761e-08 0.34221178
## accountants             12.77   9271 15.70     63.4   1171 prof  0.7825381 6.761982e-01 0.01755182
## purchasing.officers     11.42   8865  9.11     56.8   1175 prof  0.4787457 7.871214e-01 0.01454398
## chemists                14.62   8403 11.68     73.5   2111 prof  3.6997050 1.572604e-01 0.04643466
## physicists              15.64  11030  5.13     77.6   2113 prof  4.4454380 1.083142e-01 0.05381816
##                            cook
## gov.administrators  0.002428267
## general.managers    0.283269734
## accountants         0.001626121
## purchasing.officers 0.001082658
## chemists            0.013779919
## physicists          0.004882702

subset(dat, subset = cook > .5) # No Cook's D more than 0.5

##  [1] education income    women     prestige  census    type      maha_dis  maha_p    hat       cook     
## <0 rows> (or 0-length row.names)

plot(prestige.lm, 4:5) # plot 4-5 of the model shows Cook's D & leverage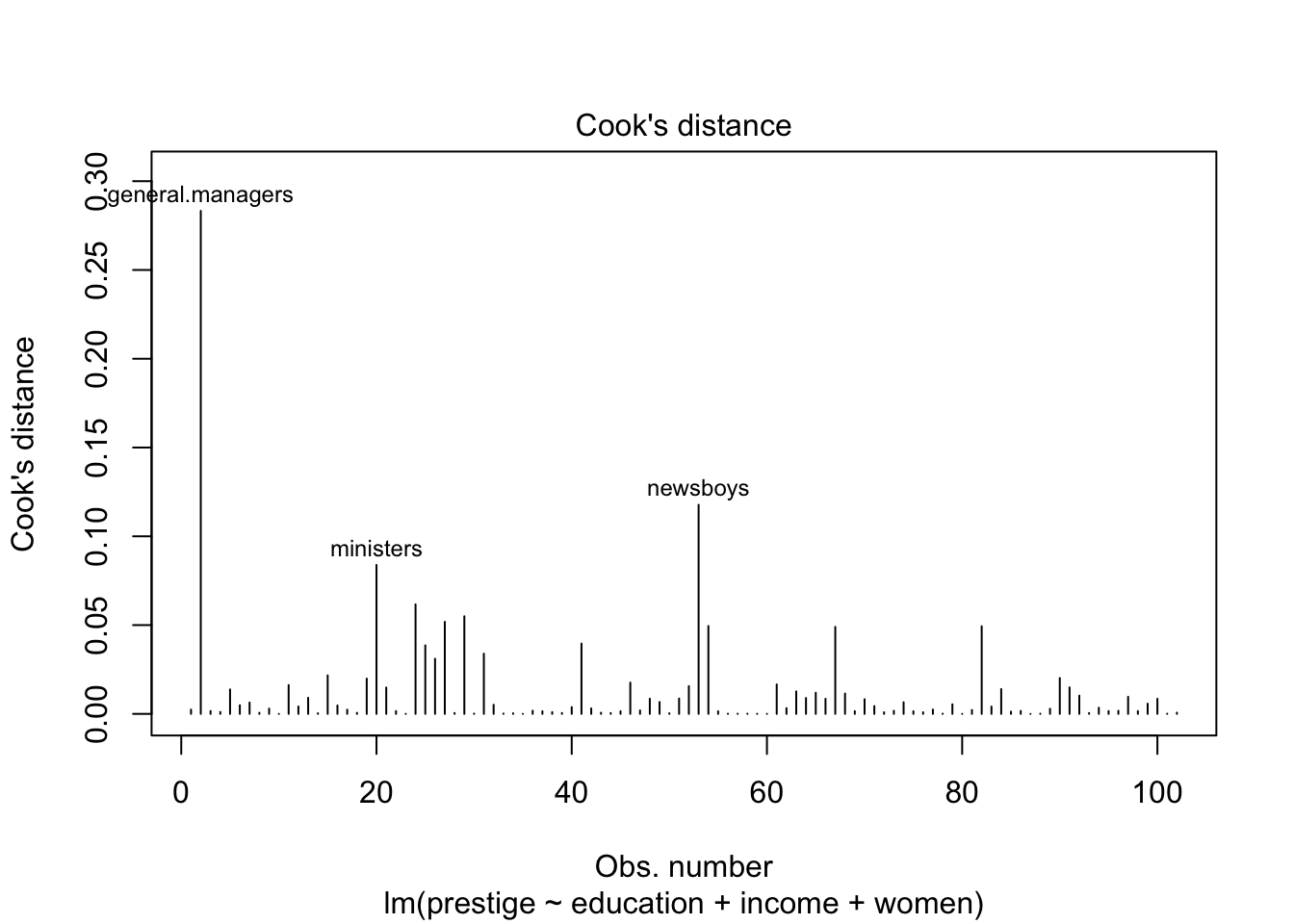

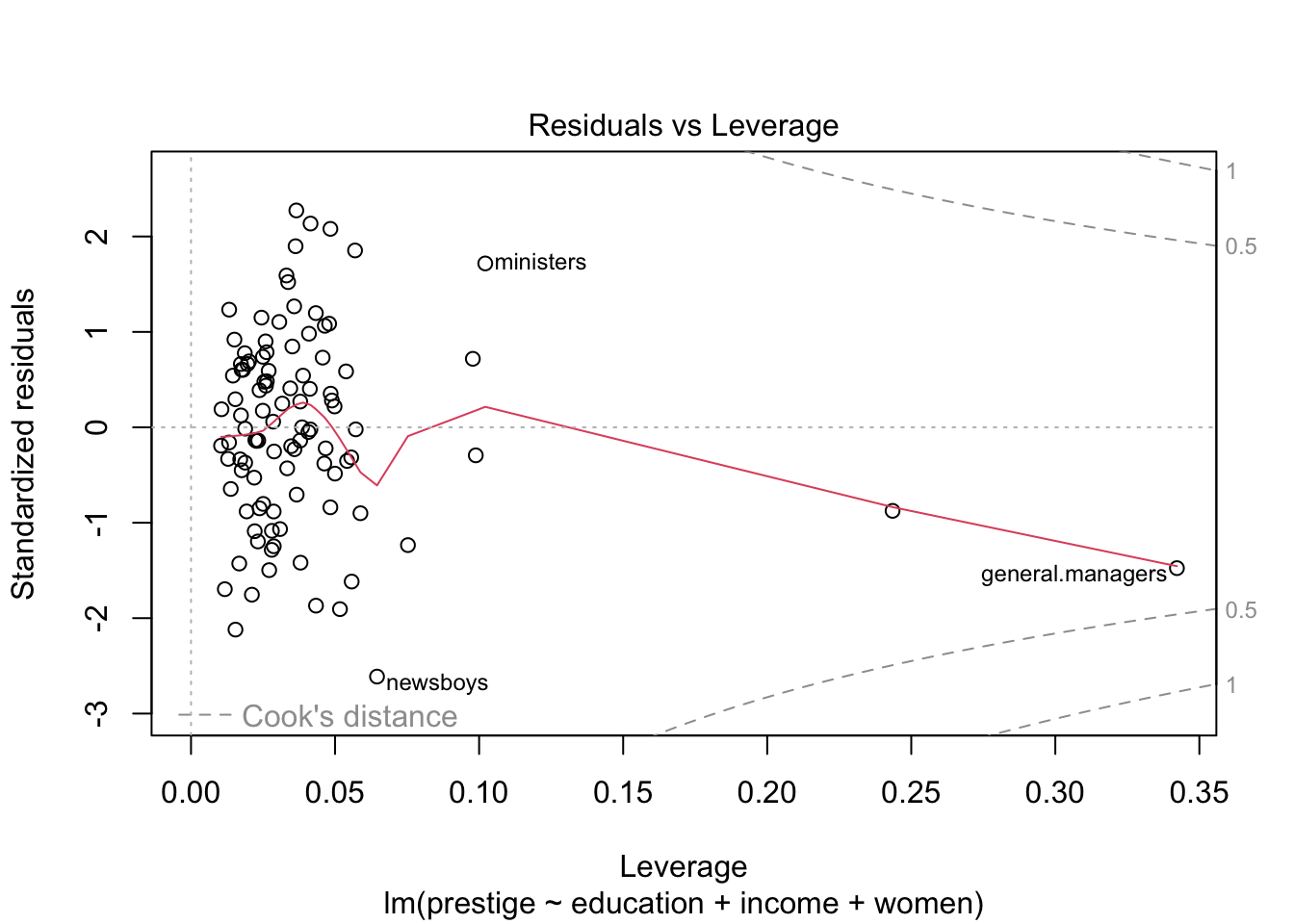
2.4 Visualizing Extreme Cases

คำสั่ง influenceIndexPlot() ใน car จะช่วย plot กราฟสำหรับตรวจสอบ influence, distance และ leverage

influenceIndexPlot(prestige.lm)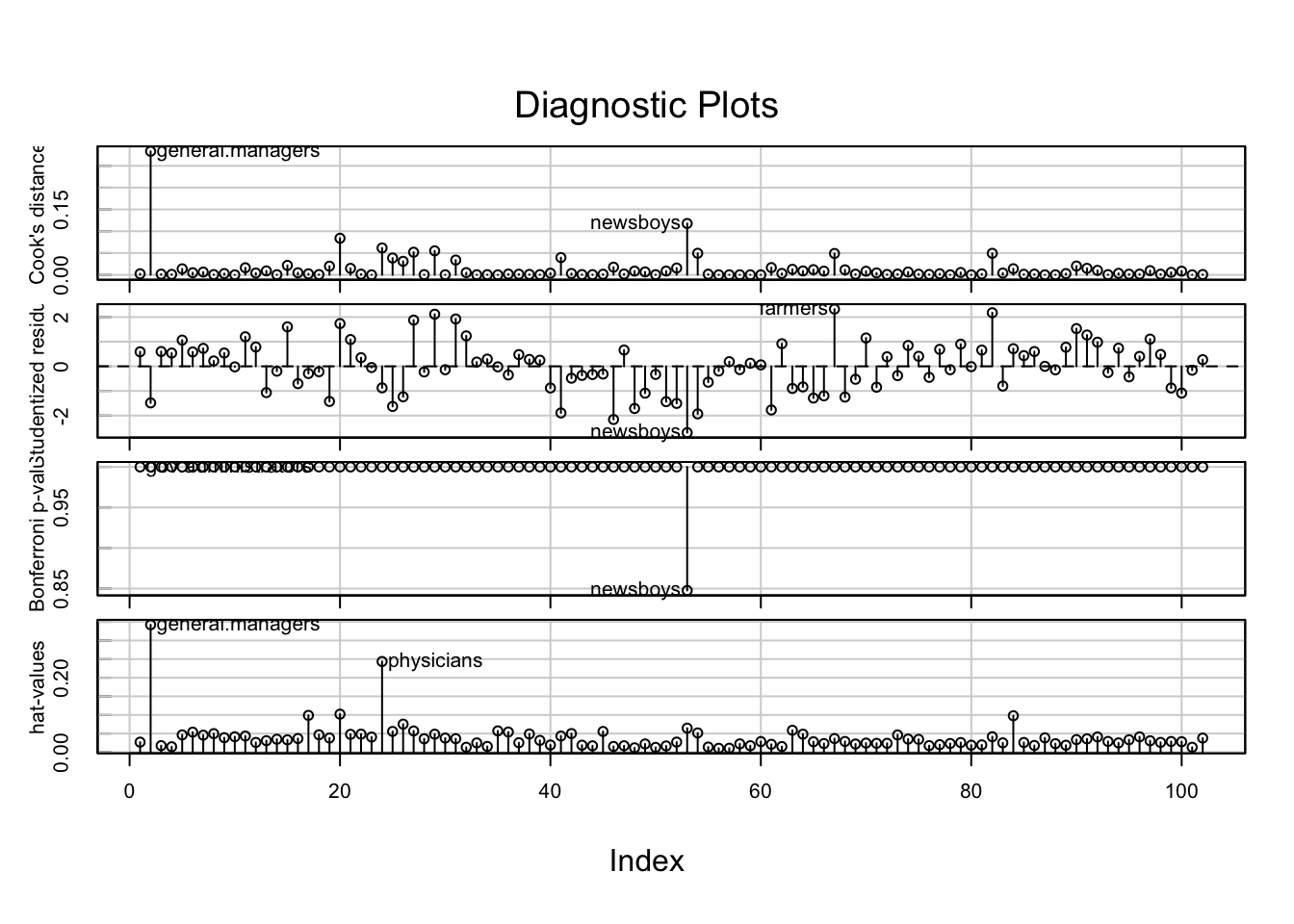

2.5 Elimination

ในการวิเคราะห์นี้ กรณีอาชีพ general.managers มีทั้ง Cook’s distance (influence) และ hat-values (distance) สูงที่สุดทั้งคู่ แต่ทว่ายังไม่ถึงเกณฑ์ที่ควรจะต้องตัดข้อมูลทิ้ง

อย่างไรก็ดีเราลองลบอาชีพนี้ออกแล้ว วิเคราะห์ใหม่ดูว่าผลเปลี่ยนไปอย่างไร

re_dat <- dat[row.names(dat) != "general.managers", ]
re.lm <- lm(prestige ~ education + income + women, re_dat)
summary(re.lm)

## 
## Call:
## lm(formula = prestige ~ education + income + women, data = re_dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -18.2210  -4.9874  -0.0928   4.9497  17.7093 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -6.4582585  3.2273074  -2.001   0.0482 *  
## education    3.9469041  0.4187139   9.426 2.33e-15 ***
## income       0.0016007  0.0003371   4.749 7.07e-06 ***
## women        0.0058119  0.0318057   0.183   0.8554    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.799 on 97 degrees of freedom
## Multiple R-squared:  0.7993, Adjusted R-squared:  0.7931 
## F-statistic: 128.8 on 3 and 97 DF,  p-value: < 2.2e-16

influenceIndexPlot(re.lm)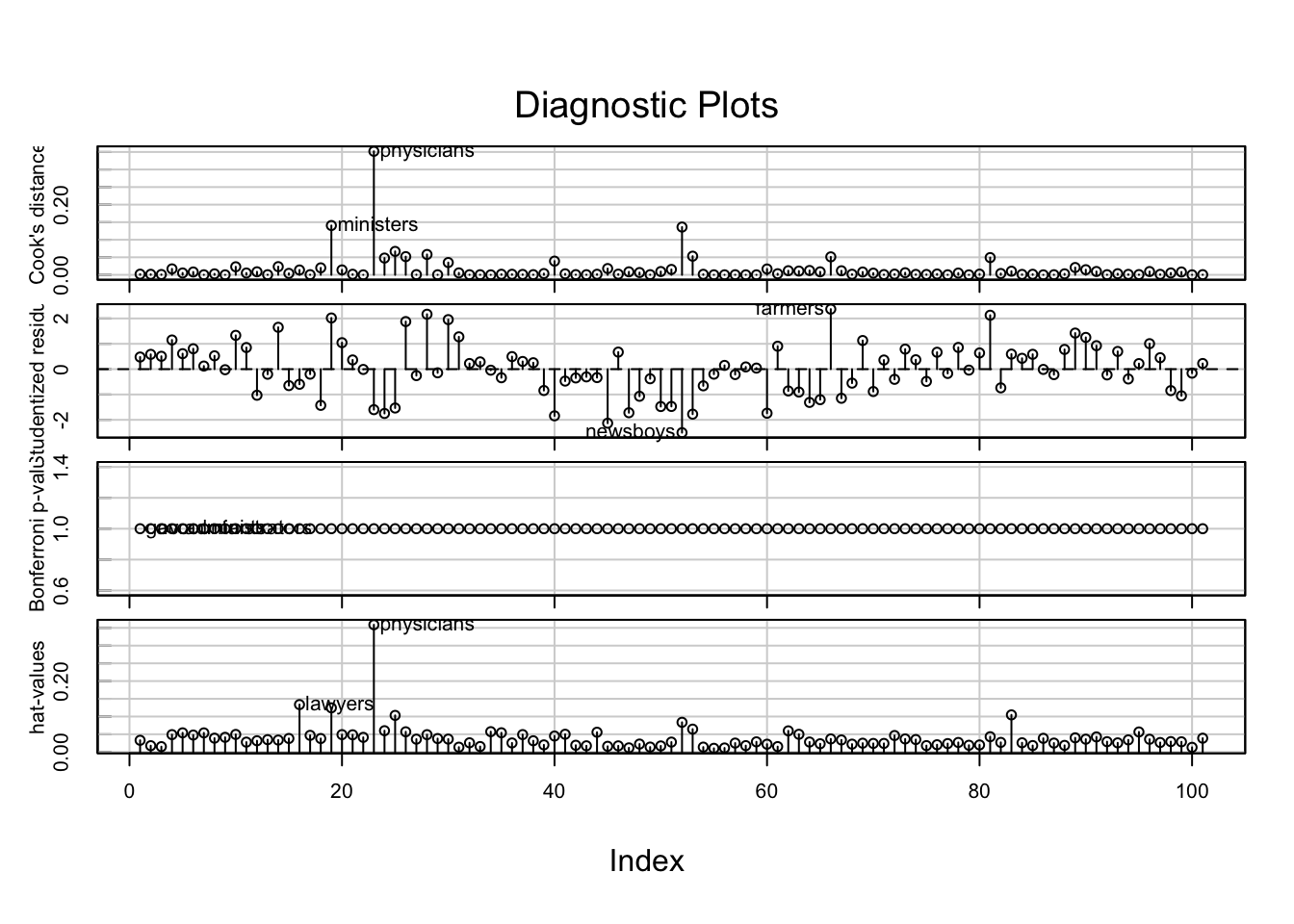

สังเกตว่าค่า \(R^2\) เพิ่มขึ้นเล็กน้อยเมื่อเทียบกับโมเดลก่อนที่จะตัดข้อมูล แสดงให้เห็นว่าการตัดข้อมูลดังกล่าวช่วยให้โมเดลอธิบายข้อมูลได้ดีขึ้น (better fit) แต่ก็เล็กน้อยมาก เพราะผลการวิเคราะห์ในภาพรวมไม่ได้มีอะไรเปลี่ยนแปลงไป ช่วยยืนยันว่าในข้อมูลชุดนี้ไม่มีเคสที่จำเป็นต้องตัดทิ้ง

3. Assumption Violation

ตรวจสอบข้อสมมติพื้นฐานของการวิเคราะห์ถดถอยแต่ละตัวด้วยคำสั่งดังต่อไปนี้

Nonlinearity

คำสั่ง crPlots() จาก car ใช้ plot เพื่อสังเกต nonlinearity ระหว่างตัวแปร X แต่ละตัวกับ Y

คำสั่ง ncvTest() ใช้ทดสอบ nonconstant variance ผลการทดสอบที่มีนัยสำคัญแสดงให้เห็นว่าความสัมพันธ์ไม่ได้คงที่เป็นเส้นตรง

#car
crPlots(prestige.lm)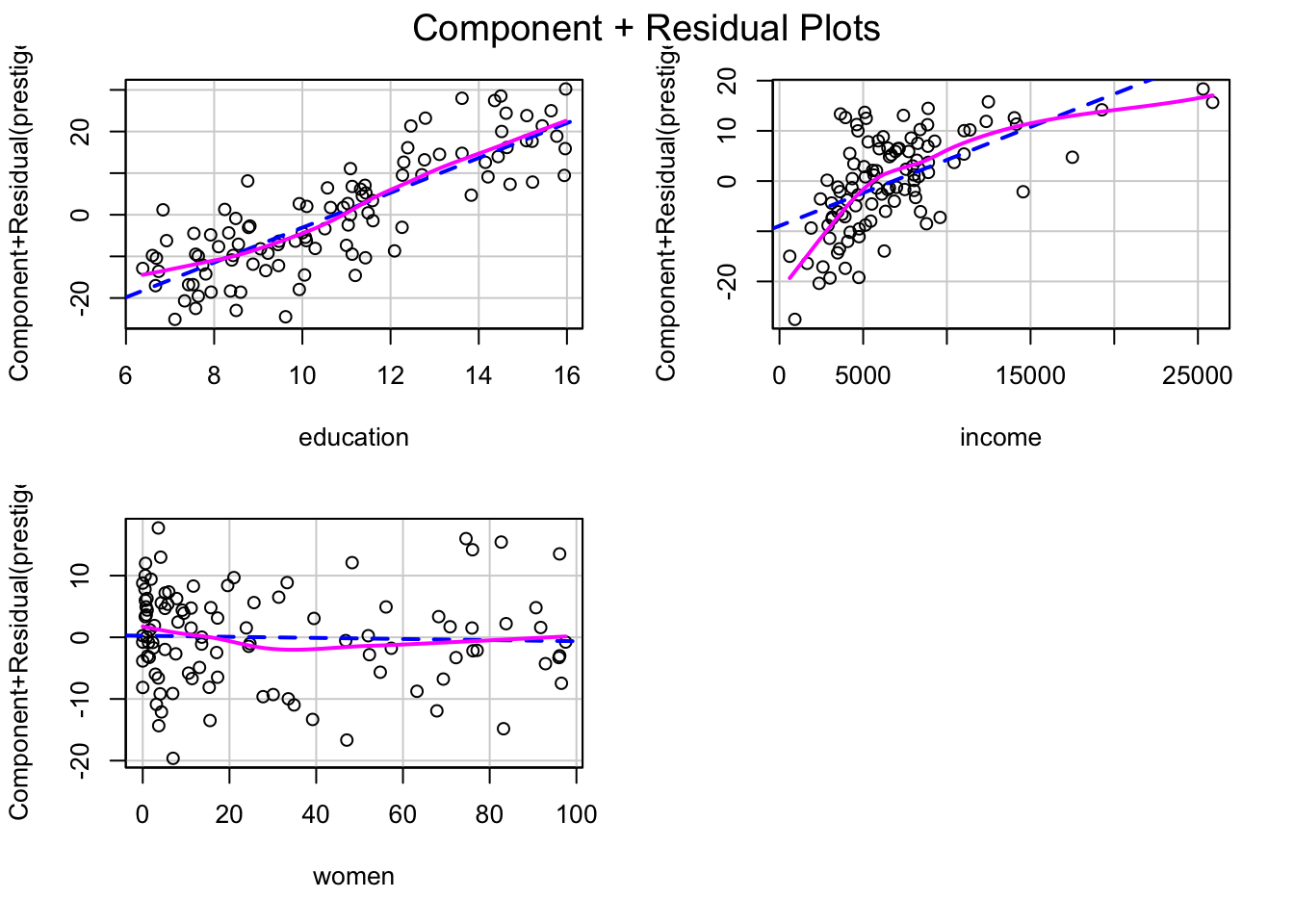

ncvTest(prestige.lm)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.2490143, Df = 1, p = 0.61777

Non-Normality

คำสั่ง qqPlot() ของ car (สังเกตว่าใช้ P ตัวใหญ่ แตกต่างจากคำสั่งของ base R) ใช้ plot เพื่อดูว่า residual กระจายตัวเป็นปกติหรือไม่

โดยปกติแล้วสถิติ F นั้นแกร่งต่อการละเมิด normality assumption ถ้าผลไม่ได้ต่างไปจาก normal มากนัก ก็สามารถวิเคราะห์ด้วย regression ได้ตามปกติ แต่ถ้าหากมีการกระจายตัวไม่เป็น normal อาจจะต้อง transform ตัวแปรบางตัวก่อน

# Base R
plot(prestige.lm, 2)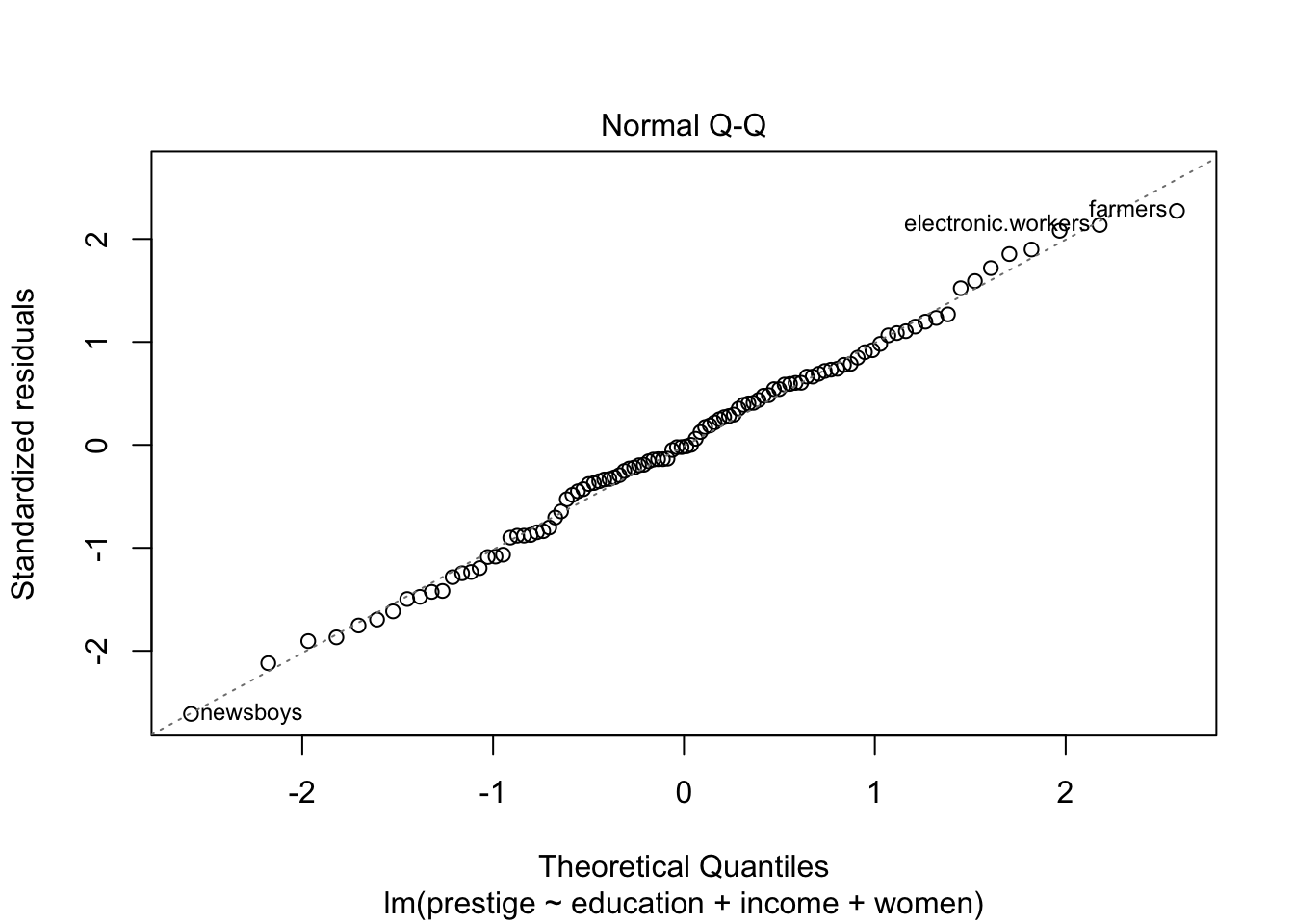

# car
car::qqPlot(prestige.lm)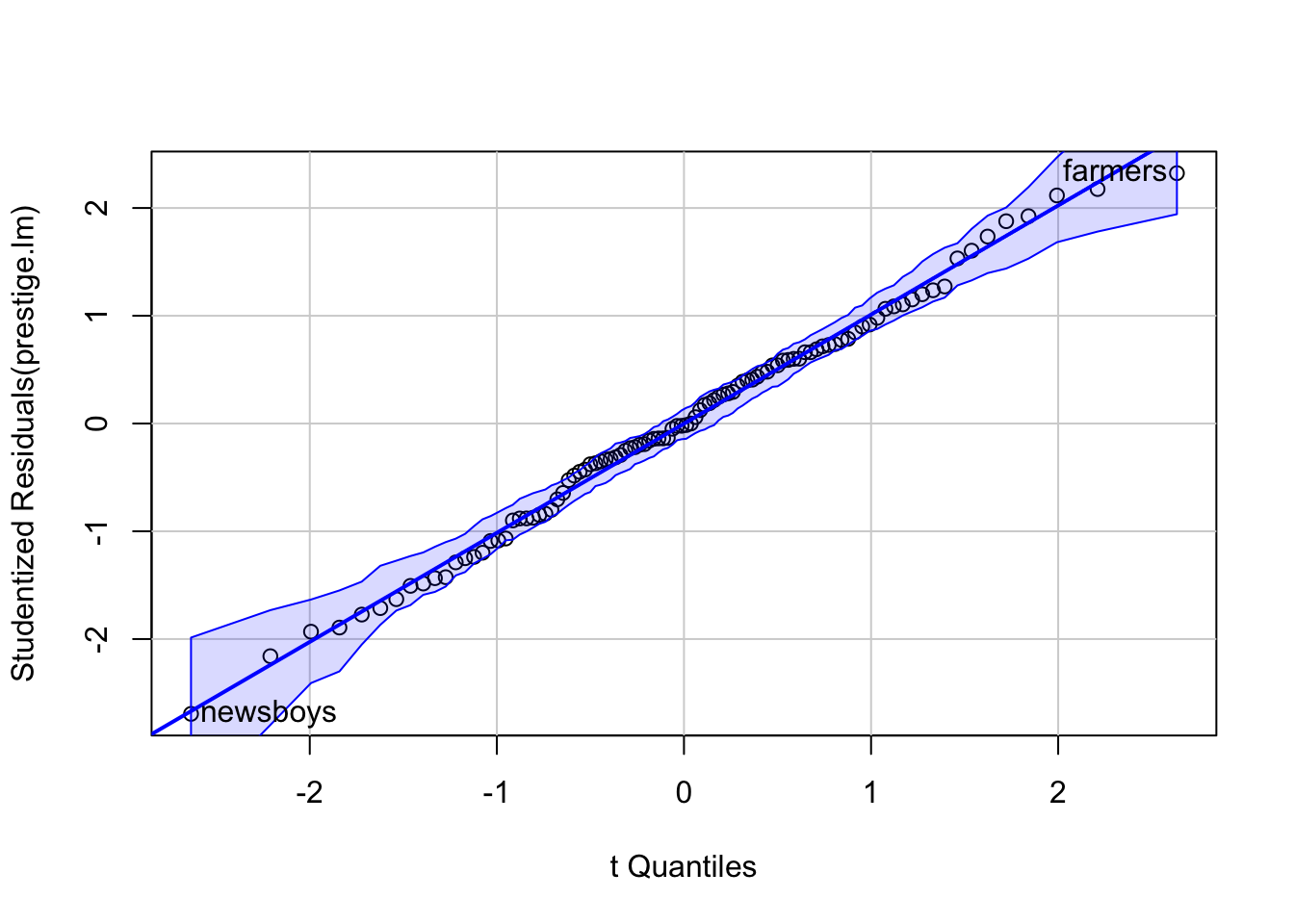

## newsboys  farmers 
##       53       67

Heteroscedasticity

การทดสอบค่าความแปรปรวนของ residual เท่าเทียมกันในทุกช่วงคะแนนทำนายหรือไม่ ใช้คำสั่ง spreadLevelPlot() ของ car

# Base R
plot(prestige.lm, 3)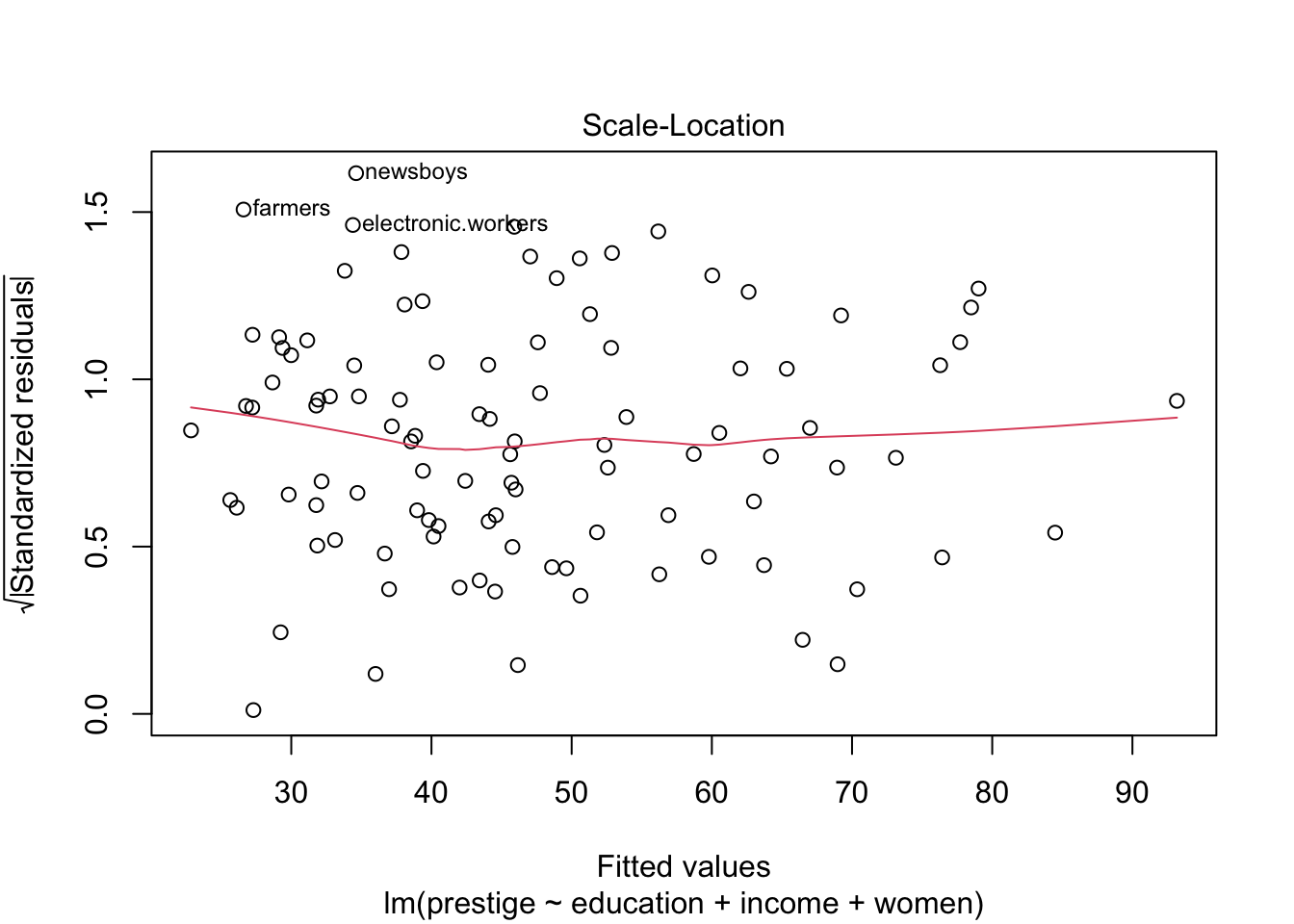

# car
spreadLevelPlot(prestige.lm)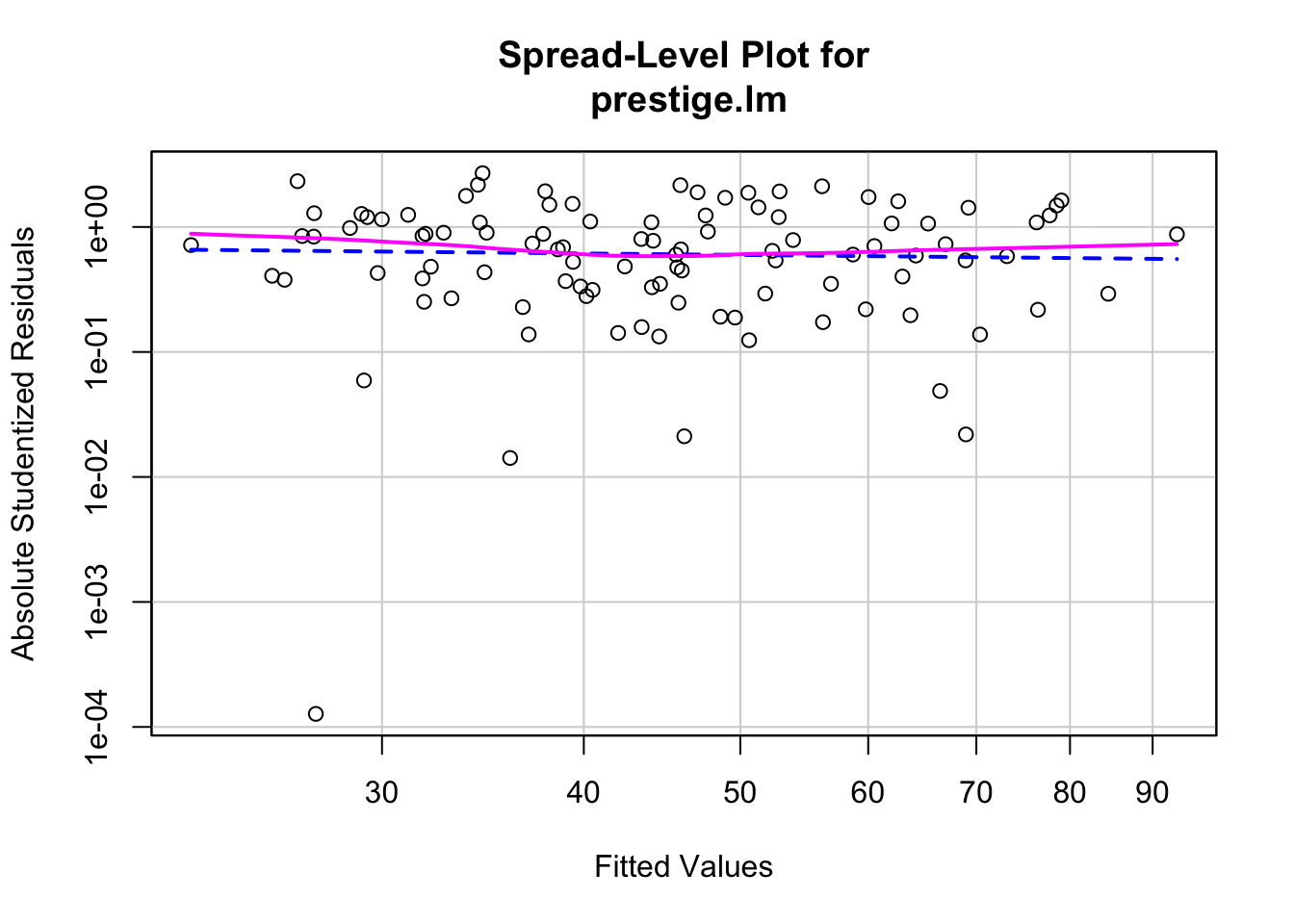

## 
## Suggested power transformation:  1.12183

Nonindependence

กรณีที่ข้อมูลของกลุ่มตัวอย่างแต่ละคนไม่เป็นอิสระจากกัน การให้ regression ปกติจะไม่เหมาะสม ควรใช้สถิติที่โมเดลข้อมูลที่ไม่เป็นอิสระจากกันได้ เช่น multi-level modeling (MLM) เป็นต้น

Multi-collinearity

อีกหนึ่ง assumption ของ regression คือ ตัวแปร X นั้นไม่สัมพันธ์กันเอง เราสามารถตรวจสอบระดับความสัมพันธ์ระหว่างตัวแปร X ในโมเดลด้วยคำสั่ง vif() ซึ่งจะทำให้ได้ค่า variance inflation factors

เกณฑ์ VIF นั้นมีหลากหลายมาก ตั้งแต่ ควรมีค่า VIF น้อยกว่า 2.5, น้อยกว่า 3, น้อยกว่า 5, น้อยกว่า 10 เป็นต้น การพิจารณาเรื่อง multi-collinearity จึงต้องพิจารณาบริบทของตัวแปรทำนายด้วยว่า มีความทับซ้อนกันมากน้อยเพียงใด เหมาะสมที่จะตัดตัวหนึ่งตัวใดออกไปหรือไม่ หรือทฤษฎีระบุไว้ว่าต้องพิจารณาทั้งสองตัวควบคู่กัน

vif(prestige.lm)

## education    income     women 
##  1.845165  2.282038  1.526593

 

---

Copyright © 2022 Kris Ariyabuddhiphongs